목차
1.FFT의 정의
2.설계 배경
3.Verilog HDL coding
4.합성
5.simualtion 검증
6.결론
2.설계 배경
3.Verilog HDL coding
4.합성
5.simualtion 검증
6.결론
본문내용
n이 소수일 경우에도 O(n log n)번의 연산 횟수를 보장한다.
쿨리-튜키 알고리즘
가장 일반적으로 사용되는 FFT 알고리즘은 쿨리-튜키 알고리즘(Cooley-Tukey algorithm)이다. 이 알고리즘은 분할 정복 알고리즘을 사용하며, 재귀적으로 n 크기의 DFT를 n = n1 n2가 성립하는 n1, n2 크기의 두 DFT로 나눈 뒤 그 결과를 O(n) 시간에 합치는 것이다. 이 방법은 1965년에 J. W. 쿨리와 J. W. 튜키가 발표하여 널리 알려졌지만, 나중에 카를 프리드리히 가우스가 1805년에 같은 방법을 이미 개발하였으며, 그 뒤에도 제한된 형태의 FFT가 종종 발견되었음이 밝혀졌다.
쿨리-튜키 알고리즘은 보통 크기 n을 재귀적으로 2등분하여 분할 정복을 적용하기 때문에 n = 2k인 경우에 많이 적용된다. 하지만 일반적으로 n1과 n2는 같을 필요가 없으며, 따라서 n이 임의의 합성수일 때에도 적용 가능하다. 쿨리-튜키 알고리즘은 DFT를 더 작은 크기의 DFT로 나누기 때문에, 뒤에 설명된 다른 FFT 알고리즘과 함께 사용될 수 있다.
원리에 관한 간단한 설명
정의에서 W = e 2π / N라고 하고 다시 정리하면,
예를 들어 N = 4일 때, 이 식을 행렬을
지수의 짝홀을 기준으로 위의 식을 다음과 같이 변형할 수 있다.
이는 다음과 같이 다시 쓸 수 있으므로, N = 4인 DFT는 N = 2인 DFT 두 개를 사용해서 계산할 수 있다.
이 과정을 재귀적으로 적용하면 N = 2k인 DFT를 O(k N) 시간 안에 할 수 있다. 이런 분할 과정을 그림으로 그리면 나비 모양의 그림이 나오기 때문에 나비 연산(Butterfly operation)이라고도 불린다.
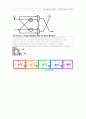
2.설계할 Radix-2 DIF 32Point FFT
< 그림 1. Radix-2 DIF 32Point FFT Flow>
다음과 같은 Flow로 설계하였다.
Twiddle Factors
엑셀을 사용하여 생성
parameter w0 =20\'b01000000000000000000;
parameter w1 =20\'b00111110111111001111;
parameter w2 =20\'b00111011001110011111;
parameter w3 =20\'b00010001101101110010;
parameter w4 =20\'b00101101011101001011;
parameter w5 =20\'b00100011101100101100;
parameter w6 =20\'b00011000011100010100;
parameter w7 =20\'b00001100011100000101;
parameter w8 =20\'b11000000011100000000;
parameter w9 =20\'b11110011111100000101;
parameter w10 =20\'b11100111111100010100;
parameter w11 =20\'b11011100101100101100;
parameter w12 =20\'b11010010111101001011;
parameter w13 =20\'b11001011001101110010;
parameter w14 =20\'b11000101001110011111;
parameter w15 =20\'b11000001011111001111;
10bit는 Cosine , 나머지 10bit Sine
각각의 MSB는 부호 bit, MSB-1bit는 정수 , 나머지는 소수로 구분하였다.
butterfly butter0( .in0(in), .in1(buffout0), .out0(add_out0), .out1(sub_out0)); //32
mux_2x1 add_mux0( .select(En0), .iA(buffout0), .iB(add_out0), .oC(add_mux_out0));
mux_2x1 sub_mux0( .select(En0), .iA(in), .iB(sub_out0), .oC(sub_mux_out0));
buff_16 buff16(.clk(clk), .rst(rst), .in(sub_mux_out0), .out(buffout0), .En(En0));
complex_multi_16 com_mul0(.clk(clk), .rst(rst), .En(En0), .in0(add_mux_out0), .out(in0));
하나의
버터플라이 - 1개
Mux - 2개
버퍼 - 1개
복소수 곱셈기 - 1개
이루어져 있다.
입력 00010001(real 1, image 0)
입력 00010001(real 1, image 0)
<임펄스 입력>
합성 결과
<전체 블록도>
앞의 16 R2SDF 모듈 중심으로 설명
<16 - R2SDF>
나머지 R2SDF 모듈도 동일 구조로 구성되어 있다.
23.5ns가 걸린 것을 알 수 있다.
Buffer 와 복소수 곱셈기 사이에서 Critical Path 가 나왔다.
이는 Buffer,복소수 곱셈기 이외에서는 register를 사용하지 않았(Pipelined 방식)기 때문이다.
좋은 곱셈 알고리즘 사용과 모듈 사이사이에 register를 삽입 한다면 더 빠른 타이밍이 나올 것이다.
<전체 Area>
<복소수 곱셈기>
전체 1705898 gate중 Buffer 부분과 복소수 곱셈부분에 많은 gate가 집중되어 있음을 확인할 수 있다.
<전체 Power>
<복소수 곱셈기 Power>
약 전체 소비 Power 0.115W 가 나왔다.
Area가 큰 부분이 Power 소비도 큼을 알 수 있다.
동일한 결과가 나왔음을 확인할 수 있다.
쿨리-튜키 알고리즘
가장 일반적으로 사용되는 FFT 알고리즘은 쿨리-튜키 알고리즘(Cooley-Tukey algorithm)이다. 이 알고리즘은 분할 정복 알고리즘을 사용하며, 재귀적으로 n 크기의 DFT를 n = n1 n2가 성립하는 n1, n2 크기의 두 DFT로 나눈 뒤 그 결과를 O(n) 시간에 합치는 것이다. 이 방법은 1965년에 J. W. 쿨리와 J. W. 튜키가 발표하여 널리 알려졌지만, 나중에 카를 프리드리히 가우스가 1805년에 같은 방법을 이미 개발하였으며, 그 뒤에도 제한된 형태의 FFT가 종종 발견되었음이 밝혀졌다.
쿨리-튜키 알고리즘은 보통 크기 n을 재귀적으로 2등분하여 분할 정복을 적용하기 때문에 n = 2k인 경우에 많이 적용된다. 하지만 일반적으로 n1과 n2는 같을 필요가 없으며, 따라서 n이 임의의 합성수일 때에도 적용 가능하다. 쿨리-튜키 알고리즘은 DFT를 더 작은 크기의 DFT로 나누기 때문에, 뒤에 설명된 다른 FFT 알고리즘과 함께 사용될 수 있다.
원리에 관한 간단한 설명
정의에서 W = e 2π / N라고 하고 다시 정리하면,
예를 들어 N = 4일 때, 이 식을 행렬을
지수의 짝홀을 기준으로 위의 식을 다음과 같이 변형할 수 있다.
이는 다음과 같이 다시 쓸 수 있으므로, N = 4인 DFT는 N = 2인 DFT 두 개를 사용해서 계산할 수 있다.
이 과정을 재귀적으로 적용하면 N = 2k인 DFT를 O(k N) 시간 안에 할 수 있다. 이런 분할 과정을 그림으로 그리면 나비 모양의 그림이 나오기 때문에 나비 연산(Butterfly operation)이라고도 불린다.
2.설계할 Radix-2 DIF 32Point FFT
< 그림 1. Radix-2 DIF 32Point FFT Flow>
다음과 같은 Flow로 설계하였다.
Twiddle Factors
엑셀을 사용하여 생성
parameter w0 =20\'b01000000000000000000;
parameter w1 =20\'b00111110111111001111;
parameter w2 =20\'b00111011001110011111;
parameter w3 =20\'b00010001101101110010;
parameter w4 =20\'b00101101011101001011;
parameter w5 =20\'b00100011101100101100;
parameter w6 =20\'b00011000011100010100;
parameter w7 =20\'b00001100011100000101;
parameter w8 =20\'b11000000011100000000;
parameter w9 =20\'b11110011111100000101;
parameter w10 =20\'b11100111111100010100;
parameter w11 =20\'b11011100101100101100;
parameter w12 =20\'b11010010111101001011;
parameter w13 =20\'b11001011001101110010;
parameter w14 =20\'b11000101001110011111;
parameter w15 =20\'b11000001011111001111;
10bit는 Cosine , 나머지 10bit Sine
각각의 MSB는 부호 bit, MSB-1bit는 정수 , 나머지는 소수로 구분하였다.
butterfly butter0( .in0(in), .in1(buffout0), .out0(add_out0), .out1(sub_out0)); //32
mux_2x1 add_mux0( .select(En0), .iA(buffout0), .iB(add_out0), .oC(add_mux_out0));
mux_2x1 sub_mux0( .select(En0), .iA(in), .iB(sub_out0), .oC(sub_mux_out0));
buff_16 buff16(.clk(clk), .rst(rst), .in(sub_mux_out0), .out(buffout0), .En(En0));
complex_multi_16 com_mul0(.clk(clk), .rst(rst), .En(En0), .in0(add_mux_out0), .out(in0));
하나의
버터플라이 - 1개
Mux - 2개
버퍼 - 1개
복소수 곱셈기 - 1개
이루어져 있다.
입력 00010001(real 1, image 0)
입력 00010001(real 1, image 0)
<임펄스 입력>
합성 결과
<전체 블록도>
앞의 16 R2SDF 모듈 중심으로 설명
<16 - R2SDF>
나머지 R2SDF 모듈도 동일 구조로 구성되어 있다.
23.5ns가 걸린 것을 알 수 있다.
Buffer 와 복소수 곱셈기 사이에서 Critical Path 가 나왔다.
이는 Buffer,복소수 곱셈기 이외에서는 register를 사용하지 않았(Pipelined 방식)기 때문이다.
좋은 곱셈 알고리즘 사용과 모듈 사이사이에 register를 삽입 한다면 더 빠른 타이밍이 나올 것이다.
<전체 Area>
<복소수 곱셈기>
전체 1705898 gate중 Buffer 부분과 복소수 곱셈부분에 많은 gate가 집중되어 있음을 확인할 수 있다.
<전체 Power>
<복소수 곱셈기 Power>
약 전체 소비 Power 0.115W 가 나왔다.
Area가 큰 부분이 Power 소비도 큼을 알 수 있다.
동일한 결과가 나왔음을 확인할 수 있다.
키워드
추천자료
 [사회 조사방법론] 연구설계(Research Design)
[사회 조사방법론] 연구설계(Research Design) [디지털설계] 블루투스에 대하여(규격,구조,연결형태,주파수,에러정정,인증,연결,응용분야,설...
[디지털설계] 블루투스에 대하여(규격,구조,연결형태,주파수,에러정정,인증,연결,응용분야,설... UWB용 Monopole Antenna 설계 및 Time domain 해석
UWB용 Monopole Antenna 설계 및 Time domain 해석 [컴퓨터구조] 32-bit ALU 설계 및 구현, CPU의 기본 구조를 C언어로 표현, 1 bit ALU부터 32 ...
[컴퓨터구조] 32-bit ALU 설계 및 구현, CPU의 기본 구조를 C언어로 표현, 1 bit ALU부터 32 ... [교수설계][교수설계 내용][교수설계 방법][교수설계 제고 방안]교수설계의 개념, 교수설계의...
[교수설계][교수설계 내용][교수설계 방법][교수설계 제고 방안]교수설계의 개념, 교수설계의... 디지털신호처리및설계(DSP)_MATLAB 프로젝트 - Final Report of Design Project
디지털신호처리및설계(DSP)_MATLAB 프로젝트 - Final Report of Design Project [컴퓨터 응용 시스템 설계 실험 보고서] verilog을 이용한 자판기 설계
[컴퓨터 응용 시스템 설계 실험 보고서] verilog을 이용한 자판기 설계 마이크로 응용설계- 도서관 좌석 시스템
마이크로 응용설계- 도서관 좌석 시스템 컴퓨터 구조 및 설계 (4판) : Computer Architecture Report
컴퓨터 구조 및 설계 (4판) : Computer Architecture Report catia 설계 산업용 공업용 선풍기 모델링 및 드래프팅 보고서 완벽
catia 설계 산업용 공업용 선풍기 모델링 및 드래프팅 보고서 완벽





























소개글