RLC의 교류회로

목차

1.실험목적

2.관련이론

3.목차

4.실험목적

5.실험순서

본문내용

=SQRT { R^2 +(X_L -X_C )^2}I_m ( { R} over { SQRT { R^2 +(X_L -X_C )^2} })sin t+ { (X_L -X_C)^2} over { SQRT { R^2 +(X_L -X_C )^2} }cos t)
= SQRT { R^2 +(X_L -X_C )^2}I_m (sin t`cos +cos t`sin )
= SQRT { R^2 +(X_L -X_C )^2}I_m sin( t+ )
=V_m sin( t+ )
(단,
V_m = SQRT { R^2 +(X_L -X_C )^2}I_m`,``` =tan^-1 { X_L -X_C} over {R }
)
위 식을 간단히 구하기 위해서는
1. L[H] 및 C[F]를 리액턴스
X_L [ ]``` 및``````X_C [ ]
으로 고친다.
즉
X_L =j L[ ]`````,X_C =-j { 1} over { C } [ ]
2. 합성 임피던스 Z[ ]을 구한다.
Z=R+J(X_L -X_C )=R+jX``,여기에서```X=X_L -X_C
가 되고 절대값
LEFT | Z RIGHT | = SQRT { R^2 +X^2}```,```위상```` =tan^-1 { X_L -X_C} over {R } =tan^-1 { X} over {R }를```` 구한다.
3. 옴의 법칙에 의해 전압 V 및 전류를 I를 계산한다.
V=ZI= SQRT { R^2 +X^2 I}`` [V]````또는`````I= { V} over {Z }= { V} over { SQRT { R^2 +X^2} }`[A]
X_L -X_C =X
를 합성 리액턴스라 하고, 임피던스의 관계를 벡터로 표시하면 그림.13와 같이 나타낸다. 합성 리액턴스 X의 값이 양과 음 또는 0으로 변화하므로 전류의 크기와 위상도 변화된다.
즉, 다음과 같은 관계가 성립한다.
1.
X_L SUCC X_C
일 때 : 유도성 회로가 되어 전압이 전류보다 만큼 앞선다.
(ELI : )
2.
X_L PREC X_C
일 때 : 용량성 회로가 되어 전류가 전압보다 만큼 앞선다.
(ICE : )
3.
X_L = X_C
일 때 : 직렬 공진 회로가 되어 전압과 전류는 동위상이 된다.
( =0 )
병렬 RCL 회로, 병렬 공진
병렬 RCL 회로망을 그림.14에 표시하였다.
V_2 =V_1
임에 유의해야 한다. 개방 회로 조건에서는 입력 어드미턴스가
Y_i`n ( )= { 1} over {R }+ { 1} over {j L }+j C = { 1} over {Z_i`n( ) }
이다.
Y_i`n( )
또는 이에 따른
Z_i`n( )
가 실수일 때 이 회로는 병렬 공잔(parallel resonance)(또는 고임피던스 공진) 상태에 있게 된다.(그래서,
LEFT | Y_i`n( ) RIGHT |
이 최소이며 따라서,
LEFT | Z_i`n( ) RIGHT |
이 최대) 이는
- { 1} over { L }+ C=0,``````즉````` = _a { 1} over { SQRT { LC} }
일 때 병렬 공진이 발생된다.
기호
_a`` 는`` { 1 } over { SQRT { LC} }
를 표시하는데 사용하여 직렬 공진(저임피던스 공진)과 구분하도록 한다. 복소 직-병렬 회로망은 여러 가지 고임피던스 공진 주파수
_a`` 를
가지며 또한, 여러 가지 저임피던스 공진 주파수
_0` 를
가진다.
정규화 임피던스는
{ Z_i`nr}over {R }= { 1} over {1+jR( C- { 1} over { L }) }
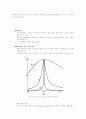
이며, 크기에 대한 주파수 응담을 그림.15에 그렸다.
이 그림에 반전력 주파수
_l``과```` _h
를 표시하였다.
직렬 공진과 유사하게, 대역폭은
=
{ _a} over {Q_a }
로 된다.
= _a
에서 병렬 회로의 양호도인
Q_a
에 대해 아래와 같이 등가 표시를 한다.
Q_a = { R} over { _a L}= _a RC=R SQRT { {C } over {L } }
RLC 병렬 회로에 교류 전압 V를 가했을 때 전전류 i를 구하면
i=i_R +i_L +i_C ``[A]
이다. 그런데
I_R = { V} over {R }``[A]
,
I_L = { V} over {X_L } = { V} over {j L }-j { V} over { L }``[A]
I_C { V} over {X_C }= { V} over { -j {1 } over { C } } =j CV``[A]
전전류 I는
I= { V} over {R } -j { V} over { L }+j CV=V( { 1} over {R } -j{1 } over { L }+j C)
=V`[ { 1} over {R } +j( C- { 1} over { L})]`[A]
따라서 전전류 I의 크기와 편각을 구하면
LEFT | I` RIGHT |= SQRT { ({ 1} over {R })^2 +( C- { 1} over { L })^2 }`V``[A]
여기서,
LEFT | Y`` RIGHT | = SQRT {( { 1} over {R })^2 +( C- { 1} over { L })^2 } ``[mho]
=tan^-1 { C- { 1} over { L } } over {R }=tan^-1 { X_C -X_L} over {R }[rad]
로 된다.
이들 관계를 어드미턴스 Y로 구하면
V=IZ= {I } over {Y }````또는``````I= { V} over {Z }=YV
가 된다.
전류 I는 다음 세 가지 경우를 생각 할 수 있다.
1.
{ 1} over { L } SUCC C
인 경우 : 유도성 회로(ELI : )
2.
{ 1} over { L } PREC C
인 경우 : 용량성 회로(ICE : )
3.
{ 1} over { L } = C
인 경우 : 병렬 공진 상태가 되어 전압과 전류는 동상이 된다.
3. 참고 자료
1. 전자개론 (상학당) 최성재 저
2. 회로망 이론 (대영사) 최진식외 4명 공저
3. 최신 회로망 이론 (한올 출판사) 한경희외 3명 공저
4. 전기전자회로실험 (정훈 출판사) 최성재

키워드

직력회로,   캐패시스턴스,   직류전류,   교류회로,   리액턴스,   직렬공진회로