생산함수에 관해

목차

1. 생산함수의 정의

2. 단기생산함수

3. 장기생산함수

4. 기술적 한계대체율체감의 법칙

5. 규모에 대한 보수

본문내용

희소성법칙 전제
·연속성, 2차미분가능성 → 수리적 표현을 위한 전제
ː특징 : 전형적인 신고전학파의 등량곡선 특징
·원점에서 멀수록 선호 → 다다익선
·우하향 → 다다익선
·교차하지 않음 → 다다익선, 이행성
·원점 볼록 → 기술적 한계대체율체감의 법칙
Q = Q(N, K)
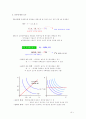
ː생산량의 증대 방향 : 그림에서 화살표 방향으로 생산량이 증대
※ 색칠된 영역의 한 점과 E점의 생산량비교 불가능
4. 기술적 한계대체율체감의 법칙-등량곡선이 원점 볼록할 조건
ː기술적 한계대체율(MRTSnk) : N투입을 한 단위 늘리면서 동일한 생산량을
을 유지하기 위해 줄여야만 되는 K의 투입량
등량곡선의 접선의 기울기
MRTSnk = |
dK over dN RIGHT|_Q0
|
K로 간접 측정한 N의 한계생산성
ː한계기술대체율체감의 법칙 : 등량곡선의 원점 볼록성 조건 ※MRS체감
※ 한계수익정보체감(균형 파라다임)
·
dMRTSnk over dN ~~ < ~~ 0
: MRTSnk와 N의 투입량이 반대로
움직임
ːMRTS체감과 MP체감 : 일반적으로 무관 ※ MRS체감과 MU체감의 무관
MRTSnk =
{M Pn} over {M Pk}
·두 요소가 독립투입물이면 필요충분조건
·등량곡선이 원점 볼록해도 MP 체증 가능
【비전형적인 등량곡선】한계기술대체율이 체감하지 않는 경우
ː완전대체재관계 : 우하향하는 직선(MRTS 일정)
예) 달구지 100대와 트럭 1대
Q = Q(N, K) = aN + bK
ː완전보완재 : 정확한 비율로 결합해야만 생산에 기여할 수 있는 투입물 관계
예) 불도저와 불도저 기사
U = min(
N over a
,
K over b
)
·
N over a
=
K over b
에서만 투입물들이 낭비없이 생산에 모두 기여(최적결합)
※ K/N = b/a
·합리적인 생산자는 최적결합비율로만 투입함(MRTS정의 안됨)
·최적결합비율 이상으로 투입한 요소는 생산성이 0
·레온티에프 생산함수 또는 고정계수 생산함수라고도함
→ 생산성이 불변임을 전제할 때 사용됨
5. 규모에 대한 보수
【동차함수】독립변수를 동일율로 변화시킬 때 다음과 같이 정리 되면 k차 동차함수
함수 : Y = f(A, B, C)
f(λA, λB, λC) = λkY
【규모의 보수】투입물을 동일물로 변화시킬 때 생산물의 변화율로 측정
·장기효율성 지표로서 궁극적으로 체감하여야 함
※동차함수를 이용하기 위하여 수학적 형식에 정의를 맞춘 예
Q = Q(N, K)
Q(λN, λK) = λkQ
ː규모의 보수 증가 : 생산량이 늘수록 장기생산효율이 증가
·K > 1 → 투입물 증대율보다 생산량 증대율이 더 높음
ː규모의 보수 불변 : 생산량이 늘어도 장기생산효율은 불변
·K = 1 → 투입물 증대율과 생산량 증대율이 동일함
※ 규모의 보수와 무관하게 수확체감은 발생(우측 그림)
ː규모의 경제 : 투입비용변화에 대하여 생산량 변화가 더 큼
·규모의 보수가 증가하는 것은 규모의 경제의 특수한 경우
ː범위의 경제 : 기술의 유사성이 존재하는 다수생산물 생산에서 효율성 증대

키워드

생산함수,   단기생산함수,   장기생산함수,   생산함수의 정의,   규모에 대한 보수,   기술적 한계대체율체감의 법칙