기계공학실험3

소개글

기계공학실험3에 대한 보고서 자료입니다.

목차

1. Fluid & Air Pressure
1) 실험 목적
2) 실험 장치
3) 실험 이론
4) 실험 방법
5) 실험 결과
6) 결과분석 및 토의
7) 참고자료

2. cam의 구동

3. Critical Velocity

4. Strain Gauge

5. Sensor

6. Beam의 처짐

본문내용

r {ρ } = { M} over {EI } = { dθ} over {ds } ~~~~~~~~~~~~ds dx,~~tanθ θ= { dy} over {dx }
{ 1} over { ρ} = { d^2`y} over {dx^2 }~~~~~~~~~~~~~~~~~~~∴~ { d^2`y} over { dx^2} =- { M} over {EI }
실험장치에 어디에 모멘트와 하중을 가할 것인지를 정하고 게이지의 눈금을 0점 조절한다.
왼쪽에서부터 오른쪽으로 X좌표로 잡고 3분의 1지점에 모멘트 10N을 걸어준다.
3분의 2지점에 2.5.10.15N의 하중을 차례로 가한다.
모멘트가 걸리는 지점에서의 처짐각을 계싼하고 2분의 1지점에서의 처짐을 계산한다.
위의 과정을 양단고정보와 양단 단순지지보에서 각각 계산한다.
Beam의 물성치
E
2.06×1011 N/m2
I
2.06×10-10 m4
L
0.9 m
양단 고정 지지보
하중 / 모멘트
2N / 10N
5N / 10N
10N / 10N
15N / 10N
Deflection(mm)
0.2 mm
0.335 mm
0.62 mm
0.9 mm
양단 단순 지지보
하중 / 모멘트
2N / 10N
5N / 10N
10N / 10N
15N / 10N
Deflection(mm)
1회
2회
3회
1회
2회
3회
1회
2회
3회
1회
2회
3회
0.57
0.63
0.58
1.31
1.29
1.28
2.51
2.465
2.42
3.64
3.59
3.56
양단 고정 지지보
하중 / 모멘트
2N / 10N
5N / 10N
10N / 10N
15N / 10N
Deflection(이론값)
0.2 mm
0.335 mm
0.62 mm
0.9 mm
Deflection(실험값)
0.186 mm
0.399 mm
0.754 mm
1.108 mm
오 차(%)
7
19
21.6
23.1
이론식 (P=2N, M0=10N×0.036m=0.36N.m)
y`` = { PL^3} over {192EI } + { M_0`a^2`b^2`(a-b)} over {2L^3`EI }
=`` { 2N×0.9^3`m^3} over {192×2.06×10^11`N/m^2`×2.06×10^-10`m^4 } + { 3.06N.m×0.6^2`m^2`×0.3^2`m^2`(0.6-0.3)m} over {2×0.9^3`m^3`×2.06×10^11`N/m^2`×2.06×10^-10`m^4}
=``0.186 mm
양단 단순 지지보
하중/모멘트
2N / 10N
5N / 10N
10N / 10N
15N / 10N
Deflection(mm)
실험값
1회
2회
3회
평균
1회
2회
3회
평균
1회
2회
3회
평균
1회
2회
3회
평균
0.57
0.63
0.58
0.59
1.31
1.29
1.28
1.29
2.51
2.465
2.42
2.47
3.64
3.59
3.56
3.60
이 론 값
0.43
1.02
2.0
2.98
오 차(%)
37
26.5
23.5
20.8
이론식 (P=2N, M0=10N×0.036m=0.36N.m)
y``=`` { 1} over {EI } × { -1} over {6 } ( { P} over {3 } - { M_0} over {l } )x^3`- { M_0} over {2 } (x- { l} over {3 } )^2`+ { P} over { 6} (x- { 2l} over { 3} )^3`+( { 4PL^3} over {81 } + { M_0`l} over {18 } )x
=`` { 1} over {2.06×10^11`×2.6×10^-10 } ({ -1} over {6 } )( { 2} over {3 } - { 0.36} over { 0.45}) 0.3^3`- { 0.36} over {2 } (0.3- { 0.45} over {3 } )^2`+
{ 2} over { 6} (0.3- { 2×0.45} over {3 } )^3`+( { 4×2×0.9^2} over { 81} + { 0.36×0.45} over { 18} )0.3~=~0.434 ``mm
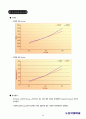
양단 고정지지보 그래프
양단 단순지지보 그래프
결과분석
실험결과에서 보는바와 같이 같은 지점에 하중과 모멘트가 작용했을 때 고정보에 비해 단순지지보에 더 큰 처짐이 일어남을 볼 수 있다.
양단 고정 지지보는 하중이 작을때(2N) 비교적 이론치와 실험치가 7%의 오차로 비교적 정확한 값을 갖지만 하중이 점점 증가할수록 오차도 따라서 점점 증가하는 것을 볼 수 있다.
양단 단순 지지보의 경우 고정보에 비해 실험치와 이론치가 비교적 큰 오차를 가지고 있으나 하중이 작을 때에 비해 하중이 증가할수록 오차는 점점 작아짐을 알 수 있다.
오차의 원인으로 가장 큰 원인으로는 게이지의 Setting을 들 수 있다. 매회 실험시마다 모멘트의 영점을 다시 잡아주었으나 그때마다 영점의 분포가 큰 것을 볼 수 있었다. 따라서 좀더 정확한 실험을 하기 위해 게이지를 교체하거나 실험횟수를 증가시키는 방법이 고려되어야 하겠다.
추를 올려놓을 때 얼마나 조심스럽게 놓느냐 또한 오차의 원인으로 들 수 있다. 추를 살며시 놓는 경우와 추를 세게 내려 놓는 경우 측정치의 오차가 많이 발생하였다.
고 찰
일반적인 공학의 응용에 있어서 beam의 설계 및 해석은 매우 중요하다. beam의 설계시 하중의 종류, 방향에 따라 그 처짐량과 처짐각을 아는 것은 회전체의 진동이나, 구조물의 안전성등의 이유로 중요한 설계요소가 되는 것이다. 그러나 실제에 있어 beam의 처짐과 처짐각을 실험을 통하여 직접 측정하기에는 어려움이 있다. 예를 들면 분포하중을 적용시키는 일이라든지, 처짐량, 처짐각을 측정하는 일은 고도의 장비를 요할 뿐만 아니라, 수많은 하중의 형태를 바뀔 때마다 다시 실험장치를 구성하는 일은 매우 어려운 일일 것이다.
따라서 실험을 통하여 구한 실험치와 이론치를 비교하여 오차를 찾고 실제 Beam에 적용하는 일은 시간과 비용을 절감하데 큰 기여를 한다.
왼쪽 설계도는 Over Head Crane(Single)으로 산업용 호이스트이다.
산업용 호이스트의 경우 상단 Beam은 양단 고정보로써 크레인이 무거운 물체를 들어올려도 원활히 움직일 수 있도록 양단 고정보로 지지된다.

키워드

유공압,   캠,   임계속도,   스트레인 게이지,   보의 처짐,   기계공학