상수도공학(인구추정5가지방법)

소개글

상수도공학(인구추정5가지방법)에 대한 보고서 자료입니다.

목차

1. 등차급수법

2. 등비급수법

3. 최소 자승법

4. 페기(peggy) 함수식에 의한 방법

5. logistic curve 방법(로지스틱 S방법, 이론 곡선법)

본문내용

▶페기(peggy) 함수식에 의한 방법 으로 구한 1990년의 추정인구는 217,836명이 된다.
5. logistic curve 방법(로지스틱 S방법, 이론 곡선법)
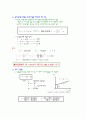
☞ 1838년 벨기에의 수학자 Verlust, P.T.는 도시인구의 증가가 변곡점을 가지고 있는
일종의 지수함수식과 잘 일치한다고 발표하고 이곡선을 logistic curve라 명명하였다.
이것은 인구가 처음에는 0에서 햇수를 거듭함에 따라 점차 증가하여, 중간에 증가율이 가장 높다가
다음에는 증가율이 점차 감소하여, 먼훗날에는 일정한 포화치에 도달하는 함수식이다.
도시의 인구동태와 잘 합치하므로 널리 사용되고 있다.
인구의 극한치를 K로 하고, 인구증가율이 극한치와 현재인구의 차에 비례한다고
보고 다음식을 얻는다.
,
여기서, y : 기준년으로부터 x년 후의 인구
x : 기준년으로부터의 경과년수
e : 자연대수의 저 (= 2.7182)
K : 포화인구
m, a, b : 상수(3점법, 최소자승법에서 구함)
※ 정수를 산정하는 데는 최소자승법과 3점법이 있으나 여기서는 최소자승법을
사용하기로한다.
위식을 변형하면
로 되며,
여기서,
로 하면
위 식은 로 된다.
여기서, 최소자승법을 사용하여 b, c (이에 따라 a가 구해진다.)의 각 정수를 구하면
(단, N : 인구의 자료수)
변곡점
인
구
증
가
경과년수
<로지스틱 곡선>
년도
x
y
K - y
xY
1980
-3
9
176,900명
333,100
5.24773
5.52257
-0.27484
0.82452
1981
-2
4
181,700명
328,300
5.25935
5.51627
-0.25692
0.51384
1982
-1
1
186,200명
323,800
5.26998
5.51028
-0.24030
0.24030
1983
0
0
191,500명
318,500
5.28217
5.50311
-0.22094
0
1984
1
1
193,400명
316,600
5.28646
5.50051
-0.21405
-0.21405
1985
2
4
198,100명
311,900
5.29688
5.49402
-0.19714
-0.39428
1986
3
9
202,800명
307,200
5.30707
5.48742
-0.18035
-0.54105
계
0
28
1330,600명
-1.58454
0.42928
, ,
▶logistic curve 방법으로 구한 1990년의 추정인구는 220266명이 된다.

키워드

등차급수법,   인구추정,   등비급수법,   최소자승법,   페기,   logistic,   상수도공학,   상수도