matlab을 이용한 깁스현상

소개글

matlab을 이용한 깁스현상에 대한 보고서 자료입니다.

목차

■ 실험

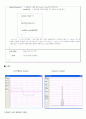
■ 그래프

■ 분석

본문내용

신호의 성분의 주파수들이 출력되는 것이기 때문에 주파수가 막대가 많아진다는 것은 주파수가 늘어남에 따라 성분이 증가한다 하여도 되겠다.
① time domain상의 파형
time domain상의 구형파는 기본주파수 50의 정수배 1, 3, 5, 7, 9의 정수배만큼의 5개의 주파수를 가진 사인파가 합쳐져서 생긴 파형으로써 모서리 부분에 최소 9%의overshoot 발생하는데, 그런 현상을 Gibbs현상이라 한다. Gibbs는 많은 정현파를 더해주면 구형파에 가깝게 나타난다는 것을 증명하였는데, 이론적으로는 overshoot되는 비율이 최소 9%로 나오게 된다.
② frequency domain상의 파형
0을 기준으로 대칭적으로 나타난것은 magnitute값을 구하는 것이 로 절대값을 사용하기 때문에 음수쪽에서 음수의 magnitute가 생성되는 것이 모두 양의 magnitute가 나타났다. 모든 막대의 합의 반은 그 신호의 주파수 성분 개수를 의미하며, 이론적으로는 0보다 큰쪽에 모든 주파수 막대가 출력되어야 하는데, DSP프로세서 안의 프로그램으로 인해 보다 보기 편하게 양쪽으로 나누어 준것이다. 디지털 상에서는 이미지 값을 표현해줄수 없기 때문이다.

키워드

matlab,   깁스,   깁스현상실험분석