철근 콘크리트 기둥 기본 핵심 이론

소개글

철근 콘크리트 기둥 기본 핵심 이론에 대한 보고서 자료입니다.

본문내용

하중의 2.5배로 취하고 계수 0.75는 1.0으로 대치한다.
2. 기둥의 종류
(1) 띠철근 기둥
(2) 나선 철근 기둥
(3) 합성 기둥
(4) 조합기둥
(5) 콘크리트로 채운 강관
3. 기둥 길이의 영향
3.1 기둥의 길이
비지지 길이 을 말하며, 부재들 사이의 순길이를 취해야 한다.
3.2 기둥의 유효길이
기둥의 강도와 거동은 기둥의 길이 뿐만 아니라 기둥 양단의 상태와 횡방향 상대 변위에 따라 다르다. 이러한 상태를 고려하여 설계를 할 때 기둥의 길이를 확대 또는 축소한 길이를 유효길이라고 하며, 장, 단주를 구별하는 세장비를 계산할 때도 사용한다.
[그림] 기둥의 종류
(1) 기둥 양단의지지 조건에 따른 유효길이
양단 힌지
일단 고정
타단 힌지
양단 고정
일단 고정
타단 자유
기둥의 종류
유효길이 계수 (k)
1.0
0.7
0.5
2.0
(2) 가로 흔들이(횡방향 상대 변위)에 따른 유효길이
a. 횡방향 상대 변위가 방지되어 있는 경우 (횡구속, non-sway): → k=1
b. 횡방향 상대 변위가 방지되어 있지 않은 경우 (비횡구속, sway):
→ k>1
3.3 기둥의 좌굴 하중
여기서,
: 유효길이계수
(양단힌지:1.0, 1단고정타단자유:0.5, 1단고정타단힌지:0.7, 양단고정:0.5)
: 기둥강성계수
: 유효길이(환산길이, 좌굴길이, 변곡점간 길이)
3.4 기둥의 좌굴 응력
여기서, : 세장비
: 최소 회전 반경
3.5 장주, 단주의 구별
이 다음 값보다 작으면 장주로 인한 영향을 무시해서 단주로 해석해도 된다.
(1) 횡방향 상대 변위가 방지되어 있는 경우 (횡구속)
세장비: 단주
(2) 횡방향 상대 변위가 방지되어 있지 않은 경우(비횡구속)
세장비: 단주
여기서, : 기둥의 비지지 길이
: 재래적인 라멘 해석에 의해 구한 압축 부재의 단모멘트 중 작은 값으로서 부재가 단일 만곡이면 (+), 복만곡이면 (-)의 부호를 가진다.
: 재래적인 라멘 해석에 의해 구한 부재 단모멘트 중의 큰 값으로서 부호는 항상 (+)이다.
[그림] 장주와 단주의 구별
- 수정R 계수법에 의한 장, 단주 구별법
(1) 가로 흔들이가 방지 되지 않은 경우, (인 경우로, )
: 단주 ( )
(2) 가로 흔들이가 방지된 경우 (인 경우로, )
: 단주 (는 기둥의 비지지 길이, 은 기둥의 유효길이)
4. 기둥의 설계
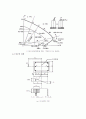
4.1 P-M 상관도
대부분의 기둥이 축력(축하중) P와 휨모멘트 M을 동시에 받는다. 이 때 기둥의 재하 능력은 축력만 작용할 때보다 떨어지므로, 축력과 모멘트의 재하 능력을 그림으로 나타낸 것을 P-M 상관도 또는 기둥의 상관도라고 한다.
[그림] P-M(축하중-모멘트) 상관도
4.2 기둥의 파괴 형태
(1) 편심거리 : 축력 P의 작용점과 기둥단면의 도심과의 거리를 말한다.
(2) 균형편심 : 콘크리트의 변형률이 극한 변형률 0.003에 달하고, 동시에 철근의 인장 응력이 항복강도 에 도달하는 상태를 균형상태라고 하고, 이때의 편심거리를 균형 편심이라고 한다.
(3) 최소 편심거리 : 편심이 작아서 축력만 작용한다고 볼 수 있는 편심 거리
(4) 파괴형태
a. 압축파괴구역 : 인 구역으로서, 기둥의 강도가 콘크리트의 압축으로 지배된다.
b. 인장 파괴 구역 : 인 구역으로서, 기둥의 강도가 철근의 인장으로 지배된다.
[그림] 기둥 단면의 설계 강도 분배
[그림] 편심하중을 받는 기둥의 P-M 상관도
4.3 단주의 설계
(a) 직사각형 기둥
(b) 원형 기둥
[그림] 단주의 극한강도 계산
(1) 나선철근기둥
a. 공칭 압축강도
b. 설계 압축강도
c. 최대 설계 압축강도
(2) 띠철근 기둥
a. 공칭압축강도
b. 설계 압축강도
c. 최대 설계 압축강도
여기서, : 강도감소계수(나선 철근 기둥:0.75, 띠철근 기둥:0.80)
: 종방향 철근의 단면적
: 기둥의 콘크리트 단면적 ()
: 편심이 0인 이상적인 기둥의 재료와 치수에 대한 공칭강도
: 부재의 중요도나 시공 등에 따른 강도의 결함을 고려한 설계 강도
: 설계시 실제로 사용하는 최대 설계 강도
4.4 장주의 설계
장주는 축력 P가 작용할 때 기둥 길이의 영향 때문에 계산된 휨모멘트보다 큰 휨모멘트가 발생한다. 따라서 모멘트 확대 계수를 사용하여 설계한다.
확대 모멘트 :
모멘트 확대 계수 :
여기서, 는 임계 하중
5. 기둥의 구조 세목
기둥의 구조세목은 다음 [표]와 같다.
[표] 기둥의 구조세목
구분
띠철근 기둥
나선 철근 기둥
단면
단면치수
최소단면 d200mm, A60,000mm2
심부지름 Dc200mm
종방향 철근 (축철근)
지름
16mm 이상
16mm 이상
개수
직사각형 단면: 4개 이상
원형 단면: 6개 이상
6개 이상
간격
40mm 이상, 150mm 이하
철근지름의 1.5배 이상
굵은 골재 최대 치수의 4/3배 이상
띠철근 기둥과 같음
철근비
1~8%
1~8%
띠철근 또는 나선철근
지름
종철근이 D32이하일 때: D10이상
종철근이 D35이상일 때: D13이상
9mm 이상
간격
종철근의 16배 이하
띠철근 지름의 48배 이하
기둥 단면의 최소 치수 이하
25~75mm
철근비
-
5.1 띠철근 기둥
(1) 종방향 철근의 철근비 제한 이유
a. 최소 1%를 두는 이유
- 너무적으면 배치 효과가 없다.
- 시공시 재료분리로 인한 부분적 결함을 보완한다.
- 예상치 않은 편심하중으로 인해 생기는 휨모멘트에 저항한다.
- 콘크리트의 크리프 및 건조수축 으로 인한 영향을 줄인다.
b. 최대 8%를 두는 이유
- 시공에 지장이 있다.
- 비경제적이 된다.
※ 겹이음되는 경우의 최대 철근비는 4%를 초과하지 않아야 한다.
(2) 띠철근의 목적
종철근의 위치를 확보하고 종철근을 횡방향으로 결속하여 좌굴을 방지한다.
5.2 나선철근기둥
(1) 나선철근의 기타 규정
a. 나선철근의 끝에서 1.5회전만큼 더 연장한다.
b. 는 400MPa 이하이다.
c. 겹침 이음할 때의 겹침이음길이 : 나선철근지름의 48배이상, 300mm이상
(2) 콘크리트 강도
나선 철근 기둥은 띠철근 기둥보다 큰 하중을 받도록 한 기둥이므로 경제적 구조로 하기 위해 콘크리트의 강도는 21MPa 이상이어야 한다.

키워드

철근,   콘크리트,   기둥,   나선,   띠,   강도,   좌굴,   세장비