디지털_논리회로_요점정리

소개글

디지털_논리회로_요점정리에 대한 보고서 자료입니다.

본문내용

출력 값, 즉 부울함수로 표현된 출력함수. 입력방정식 즉 조합논리회로의 출력은 외부입력과 플립플롭의 현재상태에 의해 결정되어 지는 값이다. 결국 입력 방정식을 구하기 위해서는 현재상태에서 다음상태로의 변화를 야기하는 입력 조건을 구하면 되고, 구해진 입력조건에 대한 부울함수 표현이 곧 입력방정식이다.
순서 논리회로의 설계는 분석과 달리 현재상태와 다음상태를 이미 알고 있기 때문에 현재상태에서 원하는 다음상태로의 변화를 일으키는 어떤 입력 조건을 알 필요가 생기는 것이다. 이와 같이 현재상태에서 다음상태로의 변화를 일으키는 입력조건의 리스트를 나타낸 것이 플립플롭의 여기표(Excitation table)이다.
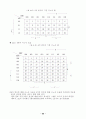
(4) 플립플롭의 여기표
여기표는 현재상태 Q(t)와 다음상태 Q(t+1), 그리고 각각의 상태 변화를 나타내게 하는 입력을 보여 준다. 현재상태에서 다음상태로의 상태변화는 모두 4가지 상태가 될 수 있고 각 상태 변화에 필요한 입력 조건은 앞에서 설명한 플립플롭의 특성표에서 구해질 수 있다. 표에서의 ×는 무의조건을 나타내는 것으로, 이때의 값은 1이나 0 둘 중의 어느 값이 되더라도 문제가 되지 않는다는 의미이다.
<표 6.5> 플립플롭의 여기표
Q(t)
Q(t+1)
S
R
0
0
0
×
0
1
1
0
1
0
0
1
1
1
×
0
Q(t)
Q(t+1)
J
K
0
0
0
×
0
1
1
×
1
0
×
1
1
1
×
0
Q(t)
Q(t+1)
D
0
0
0
0
1
1
1
0
0
1
1
1
Q(t)
Q(t+1)
T
0
0
0
0
1
1
1
0
1
1
1
0
플립플롭의 여기표에서 한가지 참고할 것은 여기표를 보면 JK플립플롭이 경우가 무의조건인 ×의 표현이 가장 많이 나타난다. 이것은 회로 설계시 입력 함수를 카노우도표를 이용하여 간소화 할 때 조합회로를 더욱 간단한 형태로 만들어 질 수 있는 것이다. 따라서 순서 논리회로의 설계시 JK플립플롭은 사용하는 것이 보다 효과적임을 알 수 있다.
제16강 6장. 순서논리회로(IV) (교재 pp.256~267)
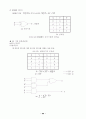
◈ D플립플롭을 이용한 설계
[그림 6.23] 설계를 위한 상태도
- 주어진 상태도로부터 플립플롭의 개수를 결정하고 기호를 부여. 상태표에서 4개의 상태가 존재하므로 두 개의 플립플롭이 필요. 두 개의 D플립플롭을 A,B , 입력과 출력을 X, Y로 표시.
- 상태도를 이용하여 상태표를 작성한다.
현재상태
입력
다음상태
출력
A
B
X
A
B
Y
0
0
0
0
0
0
0
0
1
0
1
1
0
1
0
0
0
1
0
1
1
1
0
0
1
0
0
1
0
0
1
0
1
1
1
1
1
1
0
1
1
0
1
1
1
0
0
0
- 플립플롭의 입력방정식을 구한다. D플립플롭의 경우 다음 상태의 값은 플립플롭의 입력이므로 입력방정식은 상태표의 다음상태 값으로 구해진다. 플립플롭의 입력 방정식은 상태표의 다음상태 A에 대한 최소항으로 표현되고, 플립플롭의 입력방정식은 상태표의 다음상태 B에 대한 최소항으로 표현되며 출력방정식은 Y에 대한 최소항의 표현으로 나타난다.
----(식 6.6 a)
----(식 6.6 b)
----(식 6.7)
- 구해진 입력방정식과 출력방정식을 카노우도표를 이용해 간소화 한다.
----(식 6.8 a)
----(식 6.8 b)
----(식 6.8 c)
- 간소화된 입력방정식과 출력방정식을 이용해 논리회로도를 그린다.
[그림 6.25] D플립플롭을 이용한 순서논리회로의 논리도
◈ JK플립플롭을 이용한 설계
[그림 6.26] 설계를 위한 상태도
- 플립플롭의 개수를 결정하면, 상태도에서 볼 때 4개의 상태가 존재하므로 JK플립플롭 2개가 필요하고, 각각의 플립플롭에 A, B 기호를 부여하고 입력을 X로 표시.
- 상태도로부터 상태표를 작성
현재상태
입력
다음상태
A
B
X
A
B
0
0
0
0
0
0
0
1
0
1
0
1
0
1
0
0
1
1
1
1
1
0
0
0
1
1
0
0
1
1
1
1
1
1
0
1
1
1
0
0
- 여기표가 포함된 상태표 작성
(JK플립플롭을 사용한 순서논리회로는 D플립플롭을 사용한 순서논리회로에서와 같이 상태표의 다음상태값으로 입력방정식이 구해지지 않는다. JK플립플롭에서는 주어진 현재상태에서 다음상태로의 변화를 초래시킬 수 있는 JK플립플롭이 입력조건을 알아야 한다. 이 입력조건을 알 수 있는 표가 앞에서 설명한 여기표이다. 따라서 JK플립플롭의 여기표를 참고하여 상태표를 만든다.)
조합회로의 입력
다음상태
조합회로의 출력
현재상태
입력
플립플롭 입력
A
B
X
A
B
0
0
0
0
0
0
×
0
×
0
0
1
0
1
0
×
1
×
0
1
0
1
0
1
×
×
1
0
1
1
1
1
1
×
×
0
1
0
0
0
1
×
1
1
×
1
0
1
1
1
×
0
1
×
1
1
0
1
0
×
0
×
1
1
1
1
0
0
×
1
×
1
- 입력방정식을 구함. 의 입력방정식은 상태표에서 란에 표기된 바와 같이 최소항의 표현으로 나타나고, , , 의 입력방정식도 상태표에서 각각 , , 란에 최소항으로 표현되어 다음과 같이 나타낼 수 있다.
----(식 6.9 a)
----(식 6.9 b)
----(식 6.9 c)
----(식 6.9 d)
----(식 6.9 e)
----(식 6.9 f)
----(식 6.9 g)
----(식 6.9 h)
※d로 표현된 함수는 무의조건의 항을 나타낸 것.
- 카노우도표를 이용해 간소화된 식을 구한다.
----(식 6.10 a)
----(식 6.10 b)
----(식 6.10 c)
----(식 6.10 d)
- 간소화된 입력방정식을 이용하여 논리회로도를 작성.
[그림 6.28] JK플립플롭을 이용한 순서 논리회로의 논리도
♠ 6장. 객관식 연습문제 및 풀이 (교재 pp.265~268)
1. 조합논리회로와 순서논리회로에 관한 설명으로 옳은 것은?
① 두 회로는 저장요소의 유무로서 구별할 수 없다.
② 순서논리회로는 조합회로와 저장요소로서 구성된다.
③ 조합논리회로의 출력은 저장요소의 상태 및 현재의 입력으로 결정된다.
④ 순서논리회로의 출력은 현재의 입력만 결정된다.
[해설] 조합논리회로와 순서논리회로의 가장 큰 차이는 저장요서의 유무이다. 즉, 조합논리회로는 일반산술회로, 디

키워드

디지털,   논리회로,   디지털논리