R-L-C공진회로

목차

■ 직렬공진회로

■ Q와 주파수 응답

■ 병렬공진회로

■ 병렬공진회로에서의 전류

본문내용

로로 부르기도 한다. 복소수 임피던스의 방법을 도입하여 이 회로의 전류를 구해보자.
그림 1. RLC 병렬공진회로
우선
(1)
이므로 복소수 전압은
(2)
로 놓는다. 탱크 회로의 복소수 임피던스는
(3)
이므로,
(4)
가 된다. 따라서
(5)
에서 ZT는 가 되는데, 이 때 병렬공진회로는 공진을 일으키게 된다. 식 (5)의 공진각주파수는 직렬공진회로의 경우와 같지만, 직렬공진회로에서는 L과 C의 직렬연결 부분의 임피던스가 0이 되는데 비해, 병렬공진회로에서는 L과 C의 병렬연결 부분의 임피던스는 가 된다.
병렬공진회로의 총 임피던스는
(6)
가 된다. 따라서 복소수 전류는
(7)
가 된다. 병렬공진회로에서는 탱크회로의 양단에서 출력전압을 뽑는다.
(8)
이 출력전압의 진폭은 Vo의 절대값을 취해 얻을 수 있다.
.(9)
따라서 출력전압의 유효값과 입력전압의 유효값의 비를 구하면
(10)
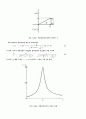
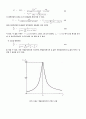
이 된다. 이 값을 주파수 의 함수로 그리면 그림 3과 같은데, 에서 공진 현상을 보이며, 이 공진주파수에서 Vo/V의 값은 1이 됨을 알 수 있다.
식 (10)을 변형하면
(11)
을 얻을 수 있다. 이를 직렬공진회로와 비교하면, 병렬공진회로의 Q 값은 직렬공진회로의 Q 값의 역수로 정의할 수 있음을 알 수 있다.
그림 2. RLC 병렬공진회로의 주파수 응답
■ 병렬공진회로에서의 전류
RLC 병렬공진회로에서 저항 R을 통해 흐르는 전류 i를 선전류(line current)라고 하고, 코일과 capacitor를 통해 흐르는 전류 iL와 iC를 순환전류(circulating current)라 한다. 임의의 시간 t에서는 Kirchhoff의 법칙에 따라
가 성립한다. 하지만, 이 세 전류의 위상이 서로 다르기 때문에 i의 유효값은 iL의 유효값과 iC의 유효값의 합이 되지는 않는다. 한 예로 공진이 일어난 경우를 생각해보자. 이 때의 선전류의 유효값은 (I는 식 (7)에 의해 주어짐)인데, 공진 때에는 0이 된다. 한편 공진 때에는 입력전압 V가 그대로 탱크회로에 걸리므로 VT = V 이고,
,(11)
(12)
가 된다. 따라서 그 유효값들은
,(13)
(14)
가 된다. 이 값들은 0이 아니며, 이므로 이 두 전류의 크기는 같다. 선전류가 0인데도 IL과 IC가 0이 아닌 것은 iL와 iC가 크기는 같고 위상차가 180 도이기 때문이다. 즉 공진 시에는 L과 C로 이루어진 loop를 순환하는 전류가 흐르게 된다.

키워드

RLC공진회로,   공진회로,   RLC,   직렬공진회로