통계의 모든 것 // 통계 어려우셨죠? 이 하나에 모든 것을 다 모았습니다// 통계 끝! (목차확인 하세요!)

소개글

통계의 모든 것 // 통계 어려우셨죠? 이 하나에 모든 것을 다 모았습니다// 통계 끝! (목차확인 하세요!)에 대한 보고서 자료입니다.

목차

1) Type of statistics

2) 자료분석 방법

3) Descriptive statistics

4) Summarizing data

5) Exploratory data analysis[EDA] checking normality

6) Transformation. 자료 변환

7) Topic6 확률 분포

8) 신뢰구간

9) 가설검증

90) Sampling distribution

91) Student's distribution (single sample) T-test

92) Student's distribution (2 sample) T-test

93) Chi-square

94) MaNemar's test for dependent sample

95) Measures of association

96) Agreement

97) Design of Experimen

98) Naming

99) ANOVA

991) Multiple comparisons

본문내용

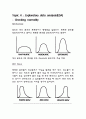
0이라는 데이터가 존재하게 되는데 이럴때는 모든 변수에 적당한 값만큼 일정 상수를 더해서 로그 변환을 한다. 이 경우 흔히 1이 사용되고, 결과의 해석에서는 1을 빼주어야한다.
왼쪽이 변환전 오른쪽이 변환후이다. 확연하게 차이가 나는 것을 알 수 있다. 이렇게 왜도가 한쪽으로 치우치는 경우에는 자연로그 변환을 통해 평주화가 가능하다. 이 데이터처럼 자연 로그에 이해 정규 분포를 가지는 경우를 lognormal distribution이라고 한다.
# Inverse transformation (역수변환)
: J모양이나, reverse J 모양일 때.
: variavle에 -1씩을 곱하고 그러고 inverse transformation을 한다.
: 최소값이 1.0이상이 되도록 한다.
-------------------------------------------------------------------------
종합
1. 오른쪽으로 꼬리(positive skewed distribution, group A transformation)가 긴 분포에서
- 로그 정규분포의 경우 로그 변환에 의해서 왜도를 교정하고
- 로그 정규분포보다 더 오른쪽으로 치우친 경우 역수로 변환하고
- 로그 정규분포보다 덜 오른쪽으로 치우친 경우 제곱근으로 변환한다.
2. 왼쪽으로 꼬리가 긴 분포(negative skewed distribution)의 경우 group B transformation이라고 하며, power transformation이라고도 한다. 이 경우 제곱 혹은 세제곱으로 변수를 변환한다.
3. 분산이 같지 않은 경우
- 평균의 차이에 비례하는 표준편차인 경우 로그변환
- 평균의 제곱에 비례하는 표준 편차인 경우 역수 변환
- 평균의 제곱근에 비례하는 표준 편차인 경우 제곱근으로 변환
-------------------------------------------------------------------------------------
# Depending on the Skewness
1) For positively skewed variables
: 최소값에 기초하여 조절.
: 최소값이 0일 경우 각 value에 1씩을 더함.
ex) 1, 3, 0, 5, 2 : positively skewed에서 min.이 0이므로 X+1을 해줘서
compute logworms = log10(worms + 1)
Compute sqrworms = SQRT(worms + 1)
: 최소값이 음수인 경우 최소값을 1로 만들 수 있는 수만큼을 더해줌.
ex) min X가 -6인 경우,
-6+6+1을 해줌.
2) For negatively skewed variables
: Original distibution을 positively skewed distribution으로 바꿔줌.
: 최대값을 빼었을 경우 1이 될수 있는 숫자만큼의 수에서 각 값의 value를 뺌. 모든 값이 0보다 큰 positively skewed distribution이 됨.
: ex) 1, 3, 0, 5, 2 : negatively skewed인 경우 최대값이 5이므로 1을 만들어 주기 위해서 6에서 각 값의 value를 빼준다.
즉, compute logworms = Log10(6-worms)
compute sqrworms = SQRT(6-worms) 로 바꿔줌.
--> 이렇게 해서 다 0이나 음수가 없고, negative skewed를 positevely로 바꿔주고나면 SQRT(y), Log(y), 1/y를 해줌.
----------------------------------------------------------------------
확률 분포 (Probability distribution)
정의
: 확률변수 x의 분포를 합이 1인 양수로 나타낸 것을 x의 확률분포
ex) T-test, chi^2, F, Binominal.
3개의 분류
: 연속형/이산형
: Bounded / unbounded 끝이 있고, 없고
: Parametric/ non-parametric
이산형일때
1) 종속 시행
: geometric, hypergeometric, inverse hypergeometric, multinomal
2) 독립시행
: Binomial distribution (이항분포)
통계학에서 정규분포와 마찬가지로 모집단이 가지는 이상적인 분포형으로 정규분포가 연속변량인 데 대하여 이항분포는 이산변량이다. 이항분포를 B(n,p)로 나타낼 때 평균값 m은 m＝np, 분산 σ2은 σ2=npq(q=1－p)임이 증명되어 있으며 p가 0이나 1에 가깝지 않고 n이 충분히 크면 이항분포는 정규분포(가우스분포)에 가까워진다는 사실도 알려져 있다.
: poission (포아선분포)
주로 시간,거리, 또는 공간상에서 무작위로 드물게 발생하는 사건의 수를 묘사하는 데 사용되고 있다. 어떤 단위구간(예, 1일)동안 이를 더 짧은 작은 단위의 구간(예, 1시간)로 나눌 수 있고 이러한 더 짧은 단위구간 중에 어떤 사건이 발생할 확률은 전체 척도 중에서 항상 일정해야 한다. 두 개 이상의 사건이 동시에 발생할 확률은 0에 가깝다. 어떤 단위구간의 사건의 발생은 다른 단위구간의 발생으로 부터 독립적이다. 특정 구간에서의 사건 발생확률은 그 구간의 크기에 비례한다.
: Negative binomial (음이항분포)
음이항 확률을 x-1번째 실험에서 r-1번째의 성공을 하고, x번째 성공을 하는 음이항 실험의 확률이다. 예를들어
------------------------------------------------------------------------------------------
연속형일때
: Normal / Studemt\'s t/ F, x^2, Exponential
-----------------------------------------------------------------------------
확률분포의 계보
이산형 - others
- Repeated Mernouli trial ----(종속시행)---- hypergeometric
----(독립

키워드

통계,   T test,   ANOVA,   Chi-square,   statistics,   확률 분포