Matlab 설계 프로젝트 - ` A / D Conversion `

소개글

Matlab 설계 프로젝트 - ` A / D Conversion `에 대한 보고서 자료입니다.

목차

1. 서론
1) A/D conversion 의 의미와 단계별 과정
2) Mathematical model for an A/D, D/A converter

2. 본론
1) Sampling
2) Quantization
3) Encoding

3. 실습 - Matlab
1) Voice Signal 의 Recoding, Writing, plotting
2) Voice Signal 의 Quantization bits 변환 (1~16bits)
3) 각 nbits 양자화된 voice signal의 음성재생 비교, plotting
4) 각 nbits 양자화된 voice signal의 Resampling, 음성재생 비교, plotting
5) Specgram을 이용한 Frequency 성분분석

4. 결론

5. 참고문헌

본문내용

uantization Signal의 1/10 DownSampling과 1/100 DownSampling 의 결과를 plotting 하였습니다. 이정도면 신호가 완전히 망가졌다고 볼수 있습니다. 실제로 1/100으로 DownSampling 을 한 Voicefile 을 재생해본 결과 음성의 세기도 확연히 떨어지고 뭉개져서 알아듣기 힘들었습니다.
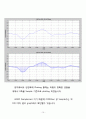
② 16bits-Quant.signal - Decimated VS 4bits-Quant.signal - Decimated
Down-Sampling rate을 증가할수록 음질의 크기는 적어지고, 음성열화도 심해지는것을 확인하였습니다. ( 음성이 둔탁해지고 겹침 = Aliasing )
5) Specgram을 이용한 Frequency 성분 분석
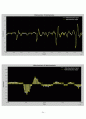
① 16bits Quant. Signal VS 4bits Quant. Signal
② 16bits Quant. Signal VS Decimated 16bits Quant. Signal by 1/20

① 16bits Quant. Signal VS 4bits Quant. Signal
16bits-Quantization Signal 과 4bits-Quantization Signal 의 Spectrum을 Plooting 하였습니다. 먼저 Specgram 에서 Y축은 Voice Frequency를 나타내기 때문에, Y축으로 많이 퍼진부분은 여러 Freq. 성분을 가지고 있는 음성들이 섞여 있다는 뜻입니다. 색상은 Power Spectrum 을 나타내는 기준이 되고, 각 시간대에서의 각 주파수의 Intensity 를 나타냅니다. 뜨겁고 진한색상일수록 큰 Intensity를 가짐을 알수 있습니다.
따라서, 16bits Quant. Signal 은 1 ~ 3.7 sec 정도까지 0 ~ 20 KHz 까지의 다양한 주파수를 가진 음성 신호들을 포함하고 있으며, 주로 저주파영역
의 밀도가 크다는것을 알수 있습니다. (0 ~ 1000 Hz) 또한 음성신호의 대부분 중요한 정보들은 이 부분에 집중되어 있음을 쉽게 생각할수 있습니다.
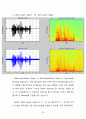
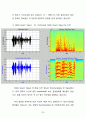
② 16bits Quant. Signal VS Decimated 16bits Quant. Signal by 1/20
16bits Quant. Signal 과 이를 1/20 정도로 DownSampling 한 Signal입니다. 먼저 왼쪽의 시간에 대한 Amplitude를 보면, 음질열화를 예상할수 있습니다. 물론 신호의 세기도 약 1/2 정도 작아짐을 확인할수 있습니다.
Freq 성분을 분석하게 되면 비교적 High Freq. 성분들이 다 잘려나갔음을 확인할수 있습니다. 이는 분명히 DownSampling 에 기인한것이며, 앞의 이론을 소개하는 과정에서 알수 있습니다. DownSampling 을 하게되면 Time Domain 에서는 Sample 들의 간격이 넓어지게 되고 (Impulse Train) 따라서 Freq. Domain 에서는 Sample 들의 간격이 좁아지기 (Impulse Train) 때문에 Convolution을 할때 Aliasing 이 생길 수밖에 없습니다. 따라서 실제 음성은 열화될 수밖에 없고 cutoff freq. 이상의 상대적으로 높은 freq. 음성 성분들은 잘려버리게 됩니다. 만약 Down-Sampling 을 할때 Anti-Aliasing을 위해 Low Pass Filter를 통과시킨다면 어느정도 Aliasing 은 피할수 있을것입니다.
또한, 지금은 다행히도 16bits-Quant. Signal을 1/20 정도로만 Down Samp
-ling 하였습니다. 원래 신호의 음성신호에서 (첫번째 Specgram) 중요한 정보가 담겨져 있는 주파수 대역은 0~1000 Hz 정도까지로 보입니다. 따라서 두 번째 신호 (Decimated Signal)에서는 비록 1000 Hz 이상의 주파수 성분을 가지고 있는 음성정보들이 잘려나갔지만 정작 중요한 정보들이 담겨져있는 정보들은 살아 남았기 때문에, 실제로 들어보면 음질의 열화는 존재할지 몰라도 알아듣는데는 이상이 없다고 생각되고 실제로 재생해서 확인하였습니다.
4. 결론
이번 Matlab 실습 Project를 통해 Analog Digital 로의 변환과정을 정확하게 이해하게 되었습니다. 먼저, 우리가 Analog 음성신호를 녹음하게 되고, 녹음된 파형을 잘게 나누어 각각의 대표 값을 추출해 그값을 녹음하면 그것이 Digital입니다. 디지털로 녹음하기 위해서는 아날로그를 디지털로 바꾸어 주는 A/D Converting 과정이 필요하며 디지털로 된 신호를 재생하기 위해서는 반대로 D/A Converting 이 필요합니다. 그리고 A/D Converting 과정에서 시간을 얼마나 잘게 쪼개느냐가 바로 Sampling Rate 입니다.
Sampling Rate은 음질과 밀접한 관계가 있으며 잘게 나눌수록 음질은 확연히 좋아짐을 확인하였습니다. 또한, 사람의 가청주파수 대역은 20 KHz 정도이며, 이부분을 모두 디지털화하려면 적어도 그 2배이상의 Sampling Rate이 필요합니다. 보통 CD가 44.1 KHz인 이유는 여기에 있는것을 알게 되었습니다. 다음으로 Quantization-bits 과정을 거칩니다. 잘게 나눈 표본값들을 일정값으로 레벨을 나누는 개념인데, 쉽게 말하면 Sound의 해상도 개념이라고 말할수 있습니다.
그리고, 바로 위의 두가지 요소가 A/D Conversion 과정을 좌우한다고 할수 있는데, 샘플수를 많이 취하고 양자화 비트수를 많이 취할수록 음질(화질) 이 좋아집니다. 즉, 같은 정보를 표현할 때 디지털 정보량이 많을수록 디지털 데이터의 품질은 확연히 높아집니다. 하지만 데이터의 정보량이 기하급수적으로 늘어나게되고, 전혀 경제적이지 못한 결과를 초래합니다. 따라서 적당히 실험적인 데이터를 적용하여 경제적인 A/D Conversion을 할 필요성이 있다는것을 알게되었습니다.
또한 Nyquist Frequency 와 Anti Aliasing Filter의 관계도 알게 되었습니다.
Nyquist Frequency 란 A/D 변환하기 이전에 Sampling Freq. 의 1/2에 해

키워드

matlab,   매틀랩,   양자화,   샘플링,   신호,   설계,   아날로그,   프로젝트