목차
1. 실험명
2. 개요및 관련이론
3. 실험목적
4. 실험방법
5. 결과 DATA
6. 결론 및 토의
2. 개요및 관련이론
3. 실험목적
4. 실험방법
5. 결과 DATA
6. 결론 및 토의
본문내용
8
6.02
11.00
5.00
5.85
10.85
R (m)
6.899
8.674
8.229
표 뉴튼링 측정값
3번에 걸친 실험을 통해 살펴본 렌즈의 곡률 반경 R은 평균 7.934m 임을 알 수 있다.
실험의 표준 편차는 1.913이었다.
6. 결론 및 토의
① 위의 실험을 통해 뉴튼링을 관찰하였다. 간섭현상은 공기층 두께의 불균형에 의해 생겨나는데 이는 실제 빛을 입사시켰을 때 렌즈를 통과하는 빛과 반사하는 빛이 다시 통과하여 이 두 빛이 경로차에 의해서 뉴튼링이 생겨났다.
실제 뉴튼링의 지름 간격을 조사하는데 있어서 실험횟수에 따라 얻어진 데이터 값은 차이가 많이 났다. 곡률 반경 R값 역시 비슷하게 나와야 하는데 차이가 많이 났다.
이는 유동 현미경을 통해 곡률 반경을 측정할 때 직접 손으로 하였고 현미경을 통해 볼 때 몸이 조금만 움직여도 상의 위치가 변하기 때문에 위와 같은 오차를 가졌다고 생각된다. 하지만 뉴튼링의 원리와 곡률반경 R의 길이를 구하는 원리를 이번 실험을 통해 확실히 배웠다.
② Biprism에 의한 간섭 원리
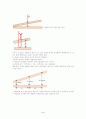
그림 Fresnel의 Biprism(이중 프리즘)에 의한 간섭현상
그림 7과 같이 이중프리즘을 사용하여 동일한 파면을 둘로 나누어 두 개의 간섭성 광원을 만들고 이들의 중첩으로 간섭무늬를 생성한다. 이중프리즘의 양끝 각 α는 대략 1도 이내이므로 굴절되어 나간다.
Fresnel의 이중 프리즘에 의한 간섭은 영의 이중실틈에 의한 간섭과 동일하다. m 번째 간섭무늬의 위치,
y_m
와 무늬 사이 간격 Δy는 다음과 같게 된다.
{ y}_{m }~ = ~{ lambda_{0}``L} over {d } LEFT ( m RIGHT )
...... 밝은 무늬
{ y}_{m }~ = ~{ lambda_{0}``L} over {d }`left( m + { 1} over {2 } right)
......어두운 무늬
DELTA ``y~=~ { { lambda }_{ 0}``L } over {d }
m = 0, 1, 2, 3, . . .
여기서 L 은 간섭하는 두 광원에서 스크린까지의 거리이고, d는 두 광원 사이의 간격이다. 초점거리를 알고 있는 렌즈를 프리즘 다음에 두고 굴절되는 두 광의 상을 스크린에 잡는다. 얇은 렌즈공식에 의하면 다음 관계식이 성립한다.
1 over a ~+~ 1 over b ~=~ 1 over f
,
m ~=~ - `` b over a ~=~ {d``\'} over d
여기서 a는 물체까지의 거리, b는 상까지의 거리, f는 초점거리, d는 물체크기, d\'는 상크기, m은 배율이다. 렌즈에서 스크린까지의 거리와 상 사이의 거리를 측정하면, 간섭하는 두 광원과 스크린까지의 거리와 두 광원 사이의 거리는 다음과 같이 결정된다.
L ~=~ a ~+~ b ~=~ {b^2 } over { b ``- `` f }
d ~=~ LEFT | `` d`\' `` b over a `` RIGHT | ~=~ LEFT | `` {d`\' ``(`b ``-``f``) } over f `` RIGHT |
6.02
11.00
5.00
5.85
10.85
R (m)
6.899
8.674
8.229
표 뉴튼링 측정값
3번에 걸친 실험을 통해 살펴본 렌즈의 곡률 반경 R은 평균 7.934m 임을 알 수 있다.
실험의 표준 편차는 1.913이었다.
6. 결론 및 토의
① 위의 실험을 통해 뉴튼링을 관찰하였다. 간섭현상은 공기층 두께의 불균형에 의해 생겨나는데 이는 실제 빛을 입사시켰을 때 렌즈를 통과하는 빛과 반사하는 빛이 다시 통과하여 이 두 빛이 경로차에 의해서 뉴튼링이 생겨났다.
실제 뉴튼링의 지름 간격을 조사하는데 있어서 실험횟수에 따라 얻어진 데이터 값은 차이가 많이 났다. 곡률 반경 R값 역시 비슷하게 나와야 하는데 차이가 많이 났다.
이는 유동 현미경을 통해 곡률 반경을 측정할 때 직접 손으로 하였고 현미경을 통해 볼 때 몸이 조금만 움직여도 상의 위치가 변하기 때문에 위와 같은 오차를 가졌다고 생각된다. 하지만 뉴튼링의 원리와 곡률반경 R의 길이를 구하는 원리를 이번 실험을 통해 확실히 배웠다.
② Biprism에 의한 간섭 원리
그림 Fresnel의 Biprism(이중 프리즘)에 의한 간섭현상
그림 7과 같이 이중프리즘을 사용하여 동일한 파면을 둘로 나누어 두 개의 간섭성 광원을 만들고 이들의 중첩으로 간섭무늬를 생성한다. 이중프리즘의 양끝 각 α는 대략 1도 이내이므로 굴절되어 나간다.
Fresnel의 이중 프리즘에 의한 간섭은 영의 이중실틈에 의한 간섭과 동일하다. m 번째 간섭무늬의 위치,
y_m
와 무늬 사이 간격 Δy는 다음과 같게 된다.
{ y}_{m }~ = ~{ lambda_{0}``L} over {d } LEFT ( m RIGHT )
...... 밝은 무늬
{ y}_{m }~ = ~{ lambda_{0}``L} over {d }`left( m + { 1} over {2 } right)
......어두운 무늬
DELTA ``y~=~ { { lambda }_{ 0}``L } over {d }
m = 0, 1, 2, 3, . . .
여기서 L 은 간섭하는 두 광원에서 스크린까지의 거리이고, d는 두 광원 사이의 간격이다. 초점거리를 알고 있는 렌즈를 프리즘 다음에 두고 굴절되는 두 광의 상을 스크린에 잡는다. 얇은 렌즈공식에 의하면 다음 관계식이 성립한다.
1 over a ~+~ 1 over b ~=~ 1 over f
,
m ~=~ - `` b over a ~=~ {d``\'} over d
여기서 a는 물체까지의 거리, b는 상까지의 거리, f는 초점거리, d는 물체크기, d\'는 상크기, m은 배율이다. 렌즈에서 스크린까지의 거리와 상 사이의 거리를 측정하면, 간섭하는 두 광원과 스크린까지의 거리와 두 광원 사이의 거리는 다음과 같이 결정된다.
L ~=~ a ~+~ b ~=~ {b^2 } over { b ``- `` f }
d ~=~ LEFT | `` d`\' `` b over a `` RIGHT | ~=~ LEFT | `` {d`\' ``(`b ``-``f``) } over f `` RIGHT |



























소개글