목차
없음
본문내용
만약 하드디스크에 데이터를 저장했다면 MOM 디렉토리에 저장된 데이터를 디스켓으로 옮기고, 하드디스크의 데이터는 지운다. 원통에 붙어 있는 실은 다음 실험반을 위하여 모두 제거시킨다.
[주의 : 새로운 측정을 할 때는 \"Q\"([Q]uit)를 눌러 프로그램을 새로 실행하도록 한다. \"N\"([N]ew)을 눌러 측정을 행할 경우 프로그램 오류가 발생하기도 한다.]
6. 실험 결과
1) 측정치
회전체 1, 2, 3의 반지름: 2.95 cm
회전체 1의 질량: 159.0 g
회전체 2의 질량: 226.2 g
회전체 3의 질량: 318.9 g
모터의 반지름: 2.5 cm
모터의 질량: 130 g
추 받침의 질량: 50 g
추 받침 위에 올린 추의 질량: 39.8 g
회전 원판의 반지름: 12.6 cm
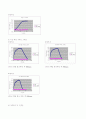
2) 시간-회전각 그래프
회전체 1 회전체 2
회전체 3
3) 시간-회전 각속도 그래프
회전체 1 회전체 2
모터의 최대 회전속력: 약 9000rpm 모터의 최대 회전속력: 약 8500rpm
회전체 3
모터의 최대 회전 속력: 약 6500rpm
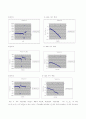
4) 각속도의 비 그래프
회전체 1 0~10초 사이 확대
회전체 2 0~10초 사이 확대
회전체 3 0~10초 사이 확대
처음 이 계의 각운동량은 0이었기 때문에 회전체, 회전원판의 각운동량을 각각 , 라 하면 이 된다. (:회전체의 회전관성, :모터 로터의 회전관성, :모터 로터+회전체의 각속도, :회전원판의 회전관성, ω:회전원판의 각속도) 이 식을 정리하면
이 되는데 우변의 값은 시간에 따라 무관하므로 각속도의 비가 일정하다면 각운동량이 보존되고 있는 것이다. 그래프 상에서 처음 나타나는 피크는 처음에 회전원판이 최대정지 마찰력을 받고있기 때문에 가속이 되지 않아서 생긴 점이라고 볼 수 있다. 그 구간을 제외하면 처음 5초간은 거의 각속도의 비가 일정하게 나타나고 있다. 이는 각운동량이 보존되고 있음을 말해주며 비가 점점 내려가는 것은 마찰에 의한 영향이다. 그러므 로 회전원판-회전체로 이루어진 이 계는 완전 고립계가 아님을 알 수 있다.
각속도비에 최대값이 나타나는 이유
라 두자. 위의 각속도 그래프의 방향을 그대로 사용하면(처음 회전체가 돌아가는 방향을 양의방향, 회전원판의 각속도의 방향을 음의 방향이라 두면) w1은 양수, w2는 음수이다. 이 계는 고립계가 아니므로 처음 상태의 각운동량이 완전 보존될 수 없다. 완전고립계가 될 수 없는 이유는 공기 마찰을 무시하면 회전원판과 베어링 사이의 마찰이다. 회전원판-회전체의 계와 여기에 지구까지 포함시키면 이것은 완전한 고립계가 이 새로운 계에서의 각운동량은 완전 보존된다. 처음 각운동량은 0이었으므로
라는 식이 성립한다. 여기서 는 지구가 가져간 각운동량으로 마찰의 방향을 생각해보면 음수가 됨을 알 수 있다. 과 은 시간이 조금 지난 후의 각속도이다. 그러면 여기서
,
이 되는데 두 번째 등식에서 우변 끝항을 보면 k<0, w2\'<0이므로 우변 끝항은 양수가 되고 결론적으로 의 각속도의 비는 처음의 양보다 작아지게 된다. 그러므로 처음 순간에 각속도의 비의 최대점이 생기게 되는 것이다. 관성 모멘트의 비를 구하기 위해서는 (식 1)이 필요한데 이것을 만족하는 점은 처음 순간, 즉 각속도의 비의 최대 점밖에 없으므로 이 값을 사용해도 무방한 것이 아니라 최대 값이 되는 순간의 각속도의 비를 이용하여 관성모멘트를 구해야 한다.
먼저, 이론상의 관성 모멘트를 구하자면,
회전체 1: =0.000069184 ()
회전체 2: =0.000098425 ()
회전체 3: =0.000138761 ()
이다, 각속도의 비가 최대가 되는 지점으로부터 실험 측정치의 관성 모멘트를 구한다. 우선, 모터의 회전 관성 모멘트는, =0.000040625 이므로, 이를 이용해서,
회전체 1: 0.000292708
회전체 2: 0.000359375
회전체 3: 0.00054761
임을 안다.
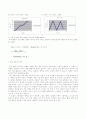
5) 각 가속도의 비
회전체 1 0~5초 사이 확대
회전체 2 0~5초 사이 확대
회전체 3 0~5초사이 확대
6) 모터의 시간-각변위 그래프 7) 모터의 시간-각속도 그래프
추가 낙하 할 때의 회전 원판의 각가속도: 10.565 rad/s^2
추+추받침의 총 질량과, 원판의 반지름, 중력 가속도, 원판의 각가속도로부터 원판의 회전 관성 모멘트를 구하면,
원판의 각가속도 = d^2θ/dt^2 = Rmg/(R^2m + I) 이므로,
이다.
∴ I=0.009069843 ()
7. 결과 토론 및 분석
이번 실험은 지금까지 해왔던 실험들 중의 최고 난이도의 실험이었다. 우선을 실험하는 것 자체가 어려웠다. 처음부터 모터가 접촉 불량이라 제대로 돌아가지 않더니, 결과로 얻은 데이터마저 우리의 기대와는 전혀 딴판으로 나왔다. 그리고, 실험하는 동안에 모터는 조용히 돌아가지 않고, 위 아래로 심하게 덜커덕거리며 세차운동을 했다.
이번 실험의 결과 정리 또한 지금까지의 모든 실험 중 가장 어려웠다. 배경이론이나 실험 방법을 보아도 제대로 된 결과 정리가 어려웠다. 위에서 한 결과 정리가 제대로 된 것인지는 모르겠으나, 지금까지의 결과를 살펴보면, 우선, 이 운동은 고립되지 않은 계에서 이루어진다는 것을 증명하고 있다. 그것은 각가속도의 비가 일정하지 않은데서 드러난다. 이것은 배경 이론에서도 배웠듯이 회전하는 모터와 회전 원판 사이에, 그리고 그 외에도 공기 등과 마찰력이 작용하기 때문이다. 그 외의 외력들 또한 이 운동에 영향을 미침으로써, 각속도의 비가 일정하지 않게 되었다. 그리고, 이론으로 구한 회전 관성 모멘트와 실험에서 측정한 회전 관성 모멘트 또한 차이가 나는데, 이것 또한 이 계가 고립되지 않은 것이라는 것을 반증한다고 할 수 있겠다. 그러나, 여러 가지 오차를 배제한다면 이 실험은 각 운동량은 보존된다는 것을 알 수 있게 하는 실험이다.
이 실험의 그래프들은 대체로 고르지 못한데, 그것은 첫째로, 실험대 자체가 기울어졌고, 그것을 수평 측정기로 맞추려 했으나, 그것 또한 제대로 되어 있지 않아서 회전판이 세차 운동을 했고, 또한, 회전 축의 표면이 매끄럽지 못한 탓으로 마찰력이 심하게 작용한 것으로 볼 수 있다.
[주의 : 새로운 측정을 할 때는 \"Q\"([Q]uit)를 눌러 프로그램을 새로 실행하도록 한다. \"N\"([N]ew)을 눌러 측정을 행할 경우 프로그램 오류가 발생하기도 한다.]
6. 실험 결과
1) 측정치
회전체 1, 2, 3의 반지름: 2.95 cm
회전체 1의 질량: 159.0 g
회전체 2의 질량: 226.2 g
회전체 3의 질량: 318.9 g
모터의 반지름: 2.5 cm
모터의 질량: 130 g
추 받침의 질량: 50 g
추 받침 위에 올린 추의 질량: 39.8 g
회전 원판의 반지름: 12.6 cm
2) 시간-회전각 그래프
회전체 1 회전체 2
회전체 3
3) 시간-회전 각속도 그래프
회전체 1 회전체 2
모터의 최대 회전속력: 약 9000rpm 모터의 최대 회전속력: 약 8500rpm
회전체 3
모터의 최대 회전 속력: 약 6500rpm
4) 각속도의 비 그래프
회전체 1 0~10초 사이 확대
회전체 2 0~10초 사이 확대
회전체 3 0~10초 사이 확대
처음 이 계의 각운동량은 0이었기 때문에 회전체, 회전원판의 각운동량을 각각 , 라 하면 이 된다. (:회전체의 회전관성, :모터 로터의 회전관성, :모터 로터+회전체의 각속도, :회전원판의 회전관성, ω:회전원판의 각속도) 이 식을 정리하면
이 되는데 우변의 값은 시간에 따라 무관하므로 각속도의 비가 일정하다면 각운동량이 보존되고 있는 것이다. 그래프 상에서 처음 나타나는 피크는 처음에 회전원판이 최대정지 마찰력을 받고있기 때문에 가속이 되지 않아서 생긴 점이라고 볼 수 있다. 그 구간을 제외하면 처음 5초간은 거의 각속도의 비가 일정하게 나타나고 있다. 이는 각운동량이 보존되고 있음을 말해주며 비가 점점 내려가는 것은 마찰에 의한 영향이다. 그러므 로 회전원판-회전체로 이루어진 이 계는 완전 고립계가 아님을 알 수 있다.
각속도비에 최대값이 나타나는 이유
라 두자. 위의 각속도 그래프의 방향을 그대로 사용하면(처음 회전체가 돌아가는 방향을 양의방향, 회전원판의 각속도의 방향을 음의 방향이라 두면) w1은 양수, w2는 음수이다. 이 계는 고립계가 아니므로 처음 상태의 각운동량이 완전 보존될 수 없다. 완전고립계가 될 수 없는 이유는 공기 마찰을 무시하면 회전원판과 베어링 사이의 마찰이다. 회전원판-회전체의 계와 여기에 지구까지 포함시키면 이것은 완전한 고립계가 이 새로운 계에서의 각운동량은 완전 보존된다. 처음 각운동량은 0이었으므로
라는 식이 성립한다. 여기서 는 지구가 가져간 각운동량으로 마찰의 방향을 생각해보면 음수가 됨을 알 수 있다. 과 은 시간이 조금 지난 후의 각속도이다. 그러면 여기서
,
이 되는데 두 번째 등식에서 우변 끝항을 보면 k<0, w2\'<0이므로 우변 끝항은 양수가 되고 결론적으로 의 각속도의 비는 처음의 양보다 작아지게 된다. 그러므로 처음 순간에 각속도의 비의 최대점이 생기게 되는 것이다. 관성 모멘트의 비를 구하기 위해서는 (식 1)이 필요한데 이것을 만족하는 점은 처음 순간, 즉 각속도의 비의 최대 점밖에 없으므로 이 값을 사용해도 무방한 것이 아니라 최대 값이 되는 순간의 각속도의 비를 이용하여 관성모멘트를 구해야 한다.
먼저, 이론상의 관성 모멘트를 구하자면,
회전체 1: =0.000069184 ()
회전체 2: =0.000098425 ()
회전체 3: =0.000138761 ()
이다, 각속도의 비가 최대가 되는 지점으로부터 실험 측정치의 관성 모멘트를 구한다. 우선, 모터의 회전 관성 모멘트는, =0.000040625 이므로, 이를 이용해서,
회전체 1: 0.000292708
회전체 2: 0.000359375
회전체 3: 0.00054761
임을 안다.
5) 각 가속도의 비
회전체 1 0~5초 사이 확대
회전체 2 0~5초 사이 확대
회전체 3 0~5초사이 확대
6) 모터의 시간-각변위 그래프 7) 모터의 시간-각속도 그래프
추가 낙하 할 때의 회전 원판의 각가속도: 10.565 rad/s^2
추+추받침의 총 질량과, 원판의 반지름, 중력 가속도, 원판의 각가속도로부터 원판의 회전 관성 모멘트를 구하면,
원판의 각가속도 = d^2θ/dt^2 = Rmg/(R^2m + I) 이므로,
이다.
∴ I=0.009069843 ()
7. 결과 토론 및 분석
이번 실험은 지금까지 해왔던 실험들 중의 최고 난이도의 실험이었다. 우선을 실험하는 것 자체가 어려웠다. 처음부터 모터가 접촉 불량이라 제대로 돌아가지 않더니, 결과로 얻은 데이터마저 우리의 기대와는 전혀 딴판으로 나왔다. 그리고, 실험하는 동안에 모터는 조용히 돌아가지 않고, 위 아래로 심하게 덜커덕거리며 세차운동을 했다.
이번 실험의 결과 정리 또한 지금까지의 모든 실험 중 가장 어려웠다. 배경이론이나 실험 방법을 보아도 제대로 된 결과 정리가 어려웠다. 위에서 한 결과 정리가 제대로 된 것인지는 모르겠으나, 지금까지의 결과를 살펴보면, 우선, 이 운동은 고립되지 않은 계에서 이루어진다는 것을 증명하고 있다. 그것은 각가속도의 비가 일정하지 않은데서 드러난다. 이것은 배경 이론에서도 배웠듯이 회전하는 모터와 회전 원판 사이에, 그리고 그 외에도 공기 등과 마찰력이 작용하기 때문이다. 그 외의 외력들 또한 이 운동에 영향을 미침으로써, 각속도의 비가 일정하지 않게 되었다. 그리고, 이론으로 구한 회전 관성 모멘트와 실험에서 측정한 회전 관성 모멘트 또한 차이가 나는데, 이것 또한 이 계가 고립되지 않은 것이라는 것을 반증한다고 할 수 있겠다. 그러나, 여러 가지 오차를 배제한다면 이 실험은 각 운동량은 보존된다는 것을 알 수 있게 하는 실험이다.
이 실험의 그래프들은 대체로 고르지 못한데, 그것은 첫째로, 실험대 자체가 기울어졌고, 그것을 수평 측정기로 맞추려 했으나, 그것 또한 제대로 되어 있지 않아서 회전판이 세차 운동을 했고, 또한, 회전 축의 표면이 매끄럽지 못한 탓으로 마찰력이 심하게 작용한 것으로 볼 수 있다.
키워드
추천자료
 [일반물리학실험] 금속막대의 영률(Young률) 측정실험 예비보고서
[일반물리학실험] 금속막대의 영률(Young률) 측정실험 예비보고서 [물리학실험]고체의 비열 측정 실험 예비, 결과 보고서
[물리학실험]고체의 비열 측정 실험 예비, 결과 보고서 [일반물리학실험] 빛의 반사와 굴절 실험 예비보고서
[일반물리학실험] 빛의 반사와 굴절 실험 예비보고서 [일반물리학실험]평행한 콘덴서 판을 이용한 쿨롱의 법칙 실험
[일반물리학실험]평행한 콘덴서 판을 이용한 쿨롱의 법칙 실험 [일반물리학실험]관성모멘트 측정 실험 예비 결과 레포트
[일반물리학실험]관성모멘트 측정 실험 예비 결과 레포트 [일반물리학실험]광섬유를 이용한 빛의 속도 측정 실험 예비 결과 레포트
[일반물리학실험]광섬유를 이용한 빛의 속도 측정 실험 예비 결과 레포트 [일반물리학실험]프랑크-헤르츠 실험 예비 결과 레포트
[일반물리학실험]프랑크-헤르츠 실험 예비 결과 레포트 [물리학실험] 광섬유를 이용한빛의속도측정 실험 결과보고서
[물리학실험] 광섬유를 이용한빛의속도측정 실험 결과보고서 [일반물리학실험] 전기 기초 실험 -예비-
[일반물리학실험] 전기 기초 실험 -예비- [물리학실험][실험레포트] 중력가속도 측정
[물리학실험][실험레포트] 중력가속도 측정 [물리학실험][실험레포트] 포물체의 운동
[물리학실험][실험레포트] 포물체의 운동 [일반물리학실험] 관성모멘트 실험 보고서
[일반물리학실험] 관성모멘트 실험 보고서  [기초전자물리학실험2] (결과) 1. 실험 장비 및 도구 사용법1 - 도통 테스터기(Conductor Tes...
[기초전자물리학실험2] (결과) 1. 실험 장비 및 도구 사용법1 - 도통 테스터기(Conductor Tes... [물리학실험2] (결과) 페러데이(Faraday)의 얼음통 실험
[물리학실험2] (결과) 페러데이(Faraday)의 얼음통 실험
































소개글