목차
1. 데이터마이닝은 데이터에서 의미를 추출하는 기법을 의미하며, 모수적 모형 접근방법과 알고리즘 접근 방법이 모두 활용될 수 있다. 모수적 모형 접근법과 알고리즘 접근법의 특징, 장단점 및 사례를 조사하시오. 또한 SNS에 게시된 텍스트 데이터를 분석한다고 할 때, 어떠한 주제를 분석하면 좋을지 주제를 제안하고 어떤 방법을 이용하여 분석하면 좋을지 데이터 마이닝 측면에서 논하시오. (7점)
2. 와인품질 데이터에 로지스틱 회귀모형을 적합하고자 한다. 과거의 분석 경험을 통해 alcohol 변수와 sulphates 두 변수가 매우 중요한 변수라는 것이 밝혀졌다고 하자. ① 이 두 변수만을 입력변수로 하여 와인 품질을 예측하는 로지스틱 회귀모형을 적합하시오. 또한, 이 적합 결과를 교재의 ② 전체 변수를 모두 넣고 분석한 결과 및 ③ 변수 선택을 하여 몇 개의 변수만 선택하고 분석한 결과와 비교하시오. (7점)
3. 입력변수와 목표변수가 모두 범주형인 어떤 데이터의 두 입력 변수 X1과 X2는 1, 2, 3 등 세 가지 값을 갖고, 목표변수는 Y=1, Y=2의 2개의 범주를 갖는다고 할 때, 각 집단별로 X1과 X2에 대하여 분할표를 아래와 같이 생성하였다. 물음에 답하시오. (8점)
(1) 분할표를 보고 이 데이터의 원형을 유추하여 생성하시오. 단, 데이터 세트의 첫째 줄에는 변수명 X1, X2, Y를 명시하시오.
(2) 지니지수를 이용하여 최초 분할 시 최적의 분리점을 찾으시오.
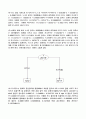
(3) 뿌리노드가 한번 분할된 분류의사결정나무를 생성하고, 두 자식노드에서 관찰치들의 집단별 빈도를 밝히시오.
(4) 위에서 생성된 분류의사결정나무(한 번만 분할)의 불순도 감소분을 계산하시오.
4. 배깅, 부스팅, 랜덤포레스트 중에서 극단값에 더 예민하게 반응할 수 있는 앙상블 방법이 무엇인지 쓰고, 교재에 설명된 각각의 알고리즘(p.116∼122)을 참고하여 그 근거를 밝히시오. (8점)
2. 와인품질 데이터에 로지스틱 회귀모형을 적합하고자 한다. 과거의 분석 경험을 통해 alcohol 변수와 sulphates 두 변수가 매우 중요한 변수라는 것이 밝혀졌다고 하자. ① 이 두 변수만을 입력변수로 하여 와인 품질을 예측하는 로지스틱 회귀모형을 적합하시오. 또한, 이 적합 결과를 교재의 ② 전체 변수를 모두 넣고 분석한 결과 및 ③ 변수 선택을 하여 몇 개의 변수만 선택하고 분석한 결과와 비교하시오. (7점)
3. 입력변수와 목표변수가 모두 범주형인 어떤 데이터의 두 입력 변수 X1과 X2는 1, 2, 3 등 세 가지 값을 갖고, 목표변수는 Y=1, Y=2의 2개의 범주를 갖는다고 할 때, 각 집단별로 X1과 X2에 대하여 분할표를 아래와 같이 생성하였다. 물음에 답하시오. (8점)
(1) 분할표를 보고 이 데이터의 원형을 유추하여 생성하시오. 단, 데이터 세트의 첫째 줄에는 변수명 X1, X2, Y를 명시하시오.
(2) 지니지수를 이용하여 최초 분할 시 최적의 분리점을 찾으시오.
(3) 뿌리노드가 한번 분할된 분류의사결정나무를 생성하고, 두 자식노드에서 관찰치들의 집단별 빈도를 밝히시오.
(4) 위에서 생성된 분류의사결정나무(한 번만 분할)의 불순도 감소분을 계산하시오.
4. 배깅, 부스팅, 랜덤포레스트 중에서 극단값에 더 예민하게 반응할 수 있는 앙상블 방법이 무엇인지 쓰고, 교재에 설명된 각각의 알고리즘(p.116∼122)을 참고하여 그 근거를 밝히시오. (8점)
본문내용
UE, use.n = TRUE, fancy = TRUE, cex=1.5)
pred <- predict(c, newdata = redata1, type=\"class\")
acc <- mean(pred==redata1$Y)
prp(c, type=4, extra=2, digits = 2, box.palette = \"auto\" )
set.seed(1234)
my.control = rpart.control(xval=10, cp=0, minsplit=20)
tree.redata1 = rpart(Y ~ X1 + X2, data=redata1, method=\"class\", control=my.control)
print(tree.redata1)
fancyRpartPlot(tree.redata1,cex=1)
1-((20/39)^2 + (19/39)^2)
1-((12/14)^2 + (2/14)^2)
1-((17/25)^2 + (8/25)^2)
결과값
n= 39
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 39 19 1 (0.5128205 0.4871795)
2) X1=3 14 2 1 (0.8571429 0.1428571) *
3) X1=1,2 25 8 2 (0.3200000 0.6800000) *
table( testpred, redata1$Y)
testpred 1 2
1 12 2
2 8 17
c$cptable
CP nsplit rel error xerror xstd
1 0.4736842 0 1.0000000 1.1052632 0.1638551
2 0.0100000 1 0.5263158 0.5263158 0.1435202
Confusion Matrix and Statistics
Reference
Prediction 1 2
1 12 2
2 8 17
Accuracy : 0.7436
95% CI : (0.5787, 0.8696)
No Information Rate : 0.5128
P-Value [Acc > NIR] : 0.002777
Kappa : 0.4909
Mcnemar\'s Test P-Value : 0.113846
Sensitivity : 0.6000
Specificity : 0.8947
Pos Pred Value : 0.8571
Neg Pred Value : 0.6800
Prevalence : 0.5128
Detection Rate : 0.3077
Detection Prevalence : 0.3590
Balanced Accuracy : 0.7474
\'Positive\' Class : 1
> 1-((20/39)^2 + (19/39)^2)
[1] 0.4996713
>
> 1-((12/14)^2 + (2/14)^2)
[1] 0.244898
>
> 1-((17/25)^2 + (8/25)^2)
[1] 0.4352
4. 앙상블 모형은 불어에서 조합하는 것이라는 뜻에서 나온 듯하다 즉 여러개의 예측모형들을 조합하여 새로운 모형을 만드는 방법으로 다중 모델 조합, 분류기 조합이라는 것이 있다. 앙상블 기법의 종류로 문제 설문에서도 나와 있듯이 배깅, 부스팅, 랜던포레스트의 방법이 가장 대표적이다. 브레이먼 이라는 학자가 제안했다고 하는 배깅은 부트스트랩과 어그리게이팅을 합성한 것으로 부트스트랩자료를 원 자료에서 생성하고 비복원추출로 다시 자료를 생성하고 이들을 모델에 넣어 실험을 한후에 계속해서 오차율을 줄이는 것을 말한다 이렇게 수정을 계속하여 최종 예측모형은 좀더 비슷한 성질을 가진 유전자가 비슷한 자료를 실험하였으므로 최종적인 예측모형에서는 오차율을 많이 줄인 모형이 될수 있다. 이러한 실험을 일부 통계학책에서는 godly play라고 하듯이 일반적인 모형을 알고 있다는 가정하에 계속적인 오차를 원래 자료와 동일한 크기의 표본을 무작위로 복원추출하여 오차를 수정하는 것으로 이후에는 여러 개의 모형으로부터 나온 결과를 보팅이라고 하는 투표과정을 거쳐서 최종 결과를 채택하는 과정을 거친다. 의사결정 나무랑 비교하였을 때 의사결정나무에서는 프루닝이라고 하는 풀모형이 아닌 가지치기를 하여 불완전하지만 어느 정도 설명력이 있는 모형을 만든다. 그러나 배깅은 가지치기 대신에 최대의 의사결정 나무를 만들고 훈련데이터를 계속적으로 랜덤 생성하여 훈련을 하여 모형을 변형하여 예측력을 향상시키는데 마치 모집단이 있는 것처럼 생각하고 이에 가장 근접한 모집단을 발견하기 위하여 계속적으로 랜덤 복원추출을 하므로 평균 예측 모형은 구할수 없지만 분산은 당연히 줄어들고 따라서 예측력은 올라간다고 할 수 있겠다.
랜덤 포레스트도 브레이먼에 의해 개발된 것이다. 랜덤 포레스트는 의사결정나무에 대한 앙상블 방법이라고 할수 있는데 의사결정나무보다 분산을 줄이고 랜덤 포레스트라는 이름에서 알수 있듯이 배깅과 부스팅보다 더 많은 임의성을 주어 설명력이 약한 모델링을 하고 이를 선형 결합하여 가장적합한 모델링을 하는 방법으로 임의성을 가진 나무에서 많은 나무를 만들어 내고 수천개의 변수를 변수제거 없이 계속 실행하여 해석이나 계산은 어렵지만 예측력은 매우 우수한 모형이다.
부스팅 방법은 프로인드와 샤파이어가 개발한 분류앙상블 방법으로 부스팅은 배깅과 유사하게 분류기를 여러개 생성하고 종합하는 방법으로 분류기를 생성하는 방식과 종합하는 방식이 다르다. 부스팅은 예측력이 약해도 여러개가 모이면 효과가 있다는 것으로 수업에서 교수님이 집단지성과 비슷하다고 말씀하신 기억이 있습니다. 이는 예측력이 약한 분류모형들을 결합하면 강한 예측력을 만드는 것으로 부스팅방법에서 가장 대표적인 것이 아다부스트방법인데 아다부스트는 가중치를 반영한 불류기 생성방식과 표본추출에 의한 분류기 생성방식이 있다. 배깅은 균등확률 부트스트랩을 사용하는데 아다부스트는 가중확률 부트스트랩을 사용한다
앙상블 방법은 오분류율을 감소시키는데 가장 큰 목표를 두고 있고 결국 이는 모형에서 오류최소화를 하는 것인데 이러한 오류에는 편향, 분산, 노이즈가 있다. 노이즈는 체계적 오차랑 비슷하게 줄이고 줄여도 결국에는 줄일수 없는 오류로 특정 지점 이후에는 더 이상 줄지
pred <- predict(c, newdata = redata1, type=\"class\")
acc <- mean(pred==redata1$Y)
prp(c, type=4, extra=2, digits = 2, box.palette = \"auto\" )
set.seed(1234)
my.control = rpart.control(xval=10, cp=0, minsplit=20)
tree.redata1 = rpart(Y ~ X1 + X2, data=redata1, method=\"class\", control=my.control)
print(tree.redata1)
fancyRpartPlot(tree.redata1,cex=1)
1-((20/39)^2 + (19/39)^2)
1-((12/14)^2 + (2/14)^2)
1-((17/25)^2 + (8/25)^2)
결과값
n= 39
node), split, n, loss, yval, (yprob)
* denotes terminal node
1) root 39 19 1 (0.5128205 0.4871795)
2) X1=3 14 2 1 (0.8571429 0.1428571) *
3) X1=1,2 25 8 2 (0.3200000 0.6800000) *
table( testpred, redata1$Y)
testpred 1 2
1 12 2
2 8 17
c$cptable
CP nsplit rel error xerror xstd
1 0.4736842 0 1.0000000 1.1052632 0.1638551
2 0.0100000 1 0.5263158 0.5263158 0.1435202
Confusion Matrix and Statistics
Reference
Prediction 1 2
1 12 2
2 8 17
Accuracy : 0.7436
95% CI : (0.5787, 0.8696)
No Information Rate : 0.5128
P-Value [Acc > NIR] : 0.002777
Kappa : 0.4909
Mcnemar\'s Test P-Value : 0.113846
Sensitivity : 0.6000
Specificity : 0.8947
Pos Pred Value : 0.8571
Neg Pred Value : 0.6800
Prevalence : 0.5128
Detection Rate : 0.3077
Detection Prevalence : 0.3590
Balanced Accuracy : 0.7474
\'Positive\' Class : 1
> 1-((20/39)^2 + (19/39)^2)
[1] 0.4996713
>
> 1-((12/14)^2 + (2/14)^2)
[1] 0.244898
>
> 1-((17/25)^2 + (8/25)^2)
[1] 0.4352
4. 앙상블 모형은 불어에서 조합하는 것이라는 뜻에서 나온 듯하다 즉 여러개의 예측모형들을 조합하여 새로운 모형을 만드는 방법으로 다중 모델 조합, 분류기 조합이라는 것이 있다. 앙상블 기법의 종류로 문제 설문에서도 나와 있듯이 배깅, 부스팅, 랜던포레스트의 방법이 가장 대표적이다. 브레이먼 이라는 학자가 제안했다고 하는 배깅은 부트스트랩과 어그리게이팅을 합성한 것으로 부트스트랩자료를 원 자료에서 생성하고 비복원추출로 다시 자료를 생성하고 이들을 모델에 넣어 실험을 한후에 계속해서 오차율을 줄이는 것을 말한다 이렇게 수정을 계속하여 최종 예측모형은 좀더 비슷한 성질을 가진 유전자가 비슷한 자료를 실험하였으므로 최종적인 예측모형에서는 오차율을 많이 줄인 모형이 될수 있다. 이러한 실험을 일부 통계학책에서는 godly play라고 하듯이 일반적인 모형을 알고 있다는 가정하에 계속적인 오차를 원래 자료와 동일한 크기의 표본을 무작위로 복원추출하여 오차를 수정하는 것으로 이후에는 여러 개의 모형으로부터 나온 결과를 보팅이라고 하는 투표과정을 거쳐서 최종 결과를 채택하는 과정을 거친다. 의사결정 나무랑 비교하였을 때 의사결정나무에서는 프루닝이라고 하는 풀모형이 아닌 가지치기를 하여 불완전하지만 어느 정도 설명력이 있는 모형을 만든다. 그러나 배깅은 가지치기 대신에 최대의 의사결정 나무를 만들고 훈련데이터를 계속적으로 랜덤 생성하여 훈련을 하여 모형을 변형하여 예측력을 향상시키는데 마치 모집단이 있는 것처럼 생각하고 이에 가장 근접한 모집단을 발견하기 위하여 계속적으로 랜덤 복원추출을 하므로 평균 예측 모형은 구할수 없지만 분산은 당연히 줄어들고 따라서 예측력은 올라간다고 할 수 있겠다.
랜덤 포레스트도 브레이먼에 의해 개발된 것이다. 랜덤 포레스트는 의사결정나무에 대한 앙상블 방법이라고 할수 있는데 의사결정나무보다 분산을 줄이고 랜덤 포레스트라는 이름에서 알수 있듯이 배깅과 부스팅보다 더 많은 임의성을 주어 설명력이 약한 모델링을 하고 이를 선형 결합하여 가장적합한 모델링을 하는 방법으로 임의성을 가진 나무에서 많은 나무를 만들어 내고 수천개의 변수를 변수제거 없이 계속 실행하여 해석이나 계산은 어렵지만 예측력은 매우 우수한 모형이다.
부스팅 방법은 프로인드와 샤파이어가 개발한 분류앙상블 방법으로 부스팅은 배깅과 유사하게 분류기를 여러개 생성하고 종합하는 방법으로 분류기를 생성하는 방식과 종합하는 방식이 다르다. 부스팅은 예측력이 약해도 여러개가 모이면 효과가 있다는 것으로 수업에서 교수님이 집단지성과 비슷하다고 말씀하신 기억이 있습니다. 이는 예측력이 약한 분류모형들을 결합하면 강한 예측력을 만드는 것으로 부스팅방법에서 가장 대표적인 것이 아다부스트방법인데 아다부스트는 가중치를 반영한 불류기 생성방식과 표본추출에 의한 분류기 생성방식이 있다. 배깅은 균등확률 부트스트랩을 사용하는데 아다부스트는 가중확률 부트스트랩을 사용한다
앙상블 방법은 오분류율을 감소시키는데 가장 큰 목표를 두고 있고 결국 이는 모형에서 오류최소화를 하는 것인데 이러한 오류에는 편향, 분산, 노이즈가 있다. 노이즈는 체계적 오차랑 비슷하게 줄이고 줄여도 결국에는 줄일수 없는 오류로 특정 지점 이후에는 더 이상 줄지
추천자료
 고령자와 장애인의 교통안전대책 문제점과 개선대책
고령자와 장애인의 교통안전대책 문제점과 개선대책 [CRM][고객관계관리][아웃소싱]CRM(고객관계관리) 현실과 도입효과 및 과제와 아웃소싱 방안(...
[CRM][고객관계관리][아웃소싱]CRM(고객관계관리) 현실과 도입효과 및 과제와 아웃소싱 방안(... [텔레마케팅][텔레마케팅 특성][텔레마케팅 현황][텔레마케팅 문제점][텔레마케팅산업 과제]...
[텔레마케팅][텔레마케팅 특성][텔레마케팅 현황][텔레마케팅 문제점][텔레마케팅산업 과제]... [데이터마이닝 등장배경][데이터마이닝 기법][데이터마이닝 문제점][미국 데이터마이닝 활용 ...
[데이터마이닝 등장배경][데이터마이닝 기법][데이터마이닝 문제점][미국 데이터마이닝 활용 ... 삼성몰 e-CRM 사례 분석
삼성몰 e-CRM 사례 분석 빅데이터의 등장배경, 활용사례, 발전과제
빅데이터의 등장배경, 활용사례, 발전과제 컴퓨터의이해 2022년 1학기] (가) 홈네트워킹과 스마트홈에 대하여 설명하라 (나) 메타버스에...
컴퓨터의이해 2022년 1학기] (가) 홈네트워킹과 스마트홈에 대하여 설명하라 (나) 메타버스에... [컴퓨터의이해 2022] 1. 홈네트워킹과 스마트홈, 메타버스, 마이크로프로세서, 2. (가) 웨어...
[컴퓨터의이해 2022] 1. 홈네트워킹과 스마트홈, 메타버스, 마이크로프로세서, 2. (가) 웨어... 엑셈 기업 분석 보고서
엑셈 기업 분석 보고서 국제경영전략
국제경영전략



































소개글