목차
---Purpose
---Amplitude Modulation
---Frequency Modulation
---Amplitude demodulation
---conclusion
---Amplitude Modulation
---Frequency Modulation
---Amplitude demodulation
---conclusion
본문내용
결과를 분석함으로써 AM 과정을 이해한다.
먼저, AM의 개념에 대해서 알아보자.
Conventional AM 신호는 large carrier component()와 double-sideband AM modulated signal() 로 구성 되어 있다. 여기서 은 message 신호이다. 즉, Conventional AM 신호는 다음 식과 같이 표현 된다.
의 조건을 만족한다면 은 항상 양수 값을 가지게 된다. 즉, AM된 모든 신호들이 양수를 가지게 되며 이로 인해 demodulation이 아주 쉽게 이루진다. DSB-AM의 이상적인 조건이 되는 것이다. 하지만, 라면 demodulation 과정이 훨씬 복잡해지고 이를 overmodulated 라 한다. 이것은 원래 DSB-AM의 단점(demodulation의 복잡성)을 그대로 가지게 되므로 Conventional AM의 사용 의미가 사라지게 된다.
즉, 을 positive 로 유지하는 게 중요하다.
식의 표현을 좀 더 간편하게 하기 위해 로 표현 할 수 있다. 여기서 은 최소값이 -1 인 nomalized signal 이고 는 modulation index라 하여 1보다 작은 상수이다. 이므로 을 항상 만족시킨다. 즉 신호는 절대overmodulated 되지 않는다.
만약 신호 라면 AM과정에서 위의 설명과 같이 신호가 overmodulated 되지만, 이 또한 conventional AM 시켜 줄 수 있다. 1 대신에 g 라는 상수를 의 최소값보다 크게 잡아주면, 은 항상 positive 하게 된다. 이 때 g 를 DC component 라고 한다.
이제 Power efficiency 가 얼마나 좋은지 소비 전력에 대해서 알아보자.
여기서 = 0 이라고 가정하면 라 할 수 있다.
위를 통해서 Conventional AM 의 Power efficiency가 많이 낮다는 것을 알 수 있다.
Conventional AM의 Power는 메시지 신호 전달 power () 뿐만 아니라 아무 의미 없는 power ()도 소비하기 때문이다. 이 아무 의미 없는 power는 carrier의 진폭과 관계있으므로 진폭이 커질수록 소비하는 의미 없는 power가 커지게 되어 power efficiency가 줄어들게 된다.
또한, 만약 DC component가 1 대신 g로 주어진다면, power efficiency는 더욱 낮아질 것이다. 의미 없는 power ()가 훨씬 증가하게 되기 때문이다.
이제 Spectrum 에 대해 알아보자.
신호에 Fourier transform 을 시켜주면 그 신호에 대한 Spectrum 을 구할 수 있다.
를 Fourier transform 을 시키면
즉, 위에서 AM의 Power 와 Spectrum을 고려해 볼때
PSD의 결과는 각 메시지 신호 해당 frequency 와 carrier frequency 에 의한 Power 가 최대치를 같는다는 것을 유추할 수 있다.
- Application : Conventional AM은 demodulation의 간편성 때문에 AM broadcasting에 일반적으로 쓰인다.
▶▶ Results with discussion
- Original Signal
이제 위에서 Matlab을 이용해서 설명했던 내용들을 구현시켜보고 하나씩 분석해가보자.
문제에서 Original Signal은 아래와 같이 주어졌다.
주어진 신호가 하나라고 볼수 있지만, 3개의 신호가 하나로 합쳐져 있다고 쉽게 접근할 수 있다.
신호1
신호2
신호3
0.25
0.25
0.5
20
10
5
우선 이 Original Signal과 그의 Power Spectral Density를 Matlab으로 구현해보자.
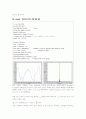
fs= 1000; % Sampling frequency
t = [0 : 1/fs :1]; % Time
s = 0.25*cos(2*pi*20*t) + 0.25*cos(2*pi*10*t) + 0.5*cos(2*pi*5*t); % The original signal
%Draw the graph of the original signal
figure(1); plot(t,s); title(\'Original Signal\');
xlabel(\'time(t)\'); ylabel(\'s(t)\');
% Draw the graph of power spectral density
fftlength = 2048*4;
figure(2); periodogram(s,[],\'onesided\',fftlength,fs) %Power spectral density
axis([0 0.03 -100 20]); % Magnify the graph to examine the result in detail
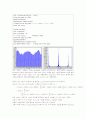
왼쪽 그래프는 문제에서 주어진 Original Signal 을 나타낸 것이다. 그래프를 보면 신호가 (-) 값을 포함하고 있다. 그러므로 Conventional AM 시켜줄 때 DC component 를 추가하여야 한다. (-)값이 0.6까지 있으므로 1정도의 DC component면 AM 신호의 모든 진폭이 (+)값으로 만드는데 충분하다.
오른쪽 그래프는 Power Spectral Density 에 대한 그림이다.
Power Spectral Density 란, 주파수에 따른 Power 를 말한다.
주파수가 5Hz, 10Hz, 20Hz에서 최대값을 가지는데 이는 위에서 설명한 신호 1,2,3 의 주파수임을 알 수 있다. 이건 Original Signal의 Spectrum에서 각 신호들의 frequency의 power가 최대임을 말하는데 메시지 전달 신호에서 Power를 소비하므로 당연한 소리이다.
원래 신호가 이다.
이것의 Spectrum (주파수에 대한 식)을 구하면
식과 그래프와 비교 했을 때, x축의 (-)좌표들이 나오지 않아 Power Spectral Density가 그림에 완전히 표현되어 있지 않다. x축의 (-)좌표들도 그림에 나타내면 위의 그림과 y출 대칭된 그림이 나타날 것이다.
식과 그래프와 비교시, 5Hz의 power 가 최대치인 이유는 S(f)에서 보면 5Hz에서 0.25의 impulse( 제일 큰 값) 을 가지기
먼저, AM의 개념에 대해서 알아보자.
Conventional AM 신호는 large carrier component()와 double-sideband AM modulated signal() 로 구성 되어 있다. 여기서 은 message 신호이다. 즉, Conventional AM 신호는 다음 식과 같이 표현 된다.
의 조건을 만족한다면 은 항상 양수 값을 가지게 된다. 즉, AM된 모든 신호들이 양수를 가지게 되며 이로 인해 demodulation이 아주 쉽게 이루진다. DSB-AM의 이상적인 조건이 되는 것이다. 하지만, 라면 demodulation 과정이 훨씬 복잡해지고 이를 overmodulated 라 한다. 이것은 원래 DSB-AM의 단점(demodulation의 복잡성)을 그대로 가지게 되므로 Conventional AM의 사용 의미가 사라지게 된다.
즉, 을 positive 로 유지하는 게 중요하다.
식의 표현을 좀 더 간편하게 하기 위해 로 표현 할 수 있다. 여기서 은 최소값이 -1 인 nomalized signal 이고 는 modulation index라 하여 1보다 작은 상수이다. 이므로 을 항상 만족시킨다. 즉 신호는 절대overmodulated 되지 않는다.
만약 신호 라면 AM과정에서 위의 설명과 같이 신호가 overmodulated 되지만, 이 또한 conventional AM 시켜 줄 수 있다. 1 대신에 g 라는 상수를 의 최소값보다 크게 잡아주면, 은 항상 positive 하게 된다. 이 때 g 를 DC component 라고 한다.
이제 Power efficiency 가 얼마나 좋은지 소비 전력에 대해서 알아보자.
여기서 = 0 이라고 가정하면 라 할 수 있다.
위를 통해서 Conventional AM 의 Power efficiency가 많이 낮다는 것을 알 수 있다.
Conventional AM의 Power는 메시지 신호 전달 power () 뿐만 아니라 아무 의미 없는 power ()도 소비하기 때문이다. 이 아무 의미 없는 power는 carrier의 진폭과 관계있으므로 진폭이 커질수록 소비하는 의미 없는 power가 커지게 되어 power efficiency가 줄어들게 된다.
또한, 만약 DC component가 1 대신 g로 주어진다면, power efficiency는 더욱 낮아질 것이다. 의미 없는 power ()가 훨씬 증가하게 되기 때문이다.
이제 Spectrum 에 대해 알아보자.
신호에 Fourier transform 을 시켜주면 그 신호에 대한 Spectrum 을 구할 수 있다.
를 Fourier transform 을 시키면
즉, 위에서 AM의 Power 와 Spectrum을 고려해 볼때
PSD의 결과는 각 메시지 신호 해당 frequency 와 carrier frequency 에 의한 Power 가 최대치를 같는다는 것을 유추할 수 있다.
- Application : Conventional AM은 demodulation의 간편성 때문에 AM broadcasting에 일반적으로 쓰인다.
▶▶ Results with discussion
- Original Signal
이제 위에서 Matlab을 이용해서 설명했던 내용들을 구현시켜보고 하나씩 분석해가보자.
문제에서 Original Signal은 아래와 같이 주어졌다.
주어진 신호가 하나라고 볼수 있지만, 3개의 신호가 하나로 합쳐져 있다고 쉽게 접근할 수 있다.
신호1
신호2
신호3
0.25
0.25
0.5
20
10
5
우선 이 Original Signal과 그의 Power Spectral Density를 Matlab으로 구현해보자.
fs= 1000; % Sampling frequency
t = [0 : 1/fs :1]; % Time
s = 0.25*cos(2*pi*20*t) + 0.25*cos(2*pi*10*t) + 0.5*cos(2*pi*5*t); % The original signal
%Draw the graph of the original signal
figure(1); plot(t,s); title(\'Original Signal\');
xlabel(\'time(t)\'); ylabel(\'s(t)\');
% Draw the graph of power spectral density
fftlength = 2048*4;
figure(2); periodogram(s,[],\'onesided\',fftlength,fs) %Power spectral density
axis([0 0.03 -100 20]); % Magnify the graph to examine the result in detail
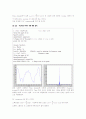
왼쪽 그래프는 문제에서 주어진 Original Signal 을 나타낸 것이다. 그래프를 보면 신호가 (-) 값을 포함하고 있다. 그러므로 Conventional AM 시켜줄 때 DC component 를 추가하여야 한다. (-)값이 0.6까지 있으므로 1정도의 DC component면 AM 신호의 모든 진폭이 (+)값으로 만드는데 충분하다.
오른쪽 그래프는 Power Spectral Density 에 대한 그림이다.
Power Spectral Density 란, 주파수에 따른 Power 를 말한다.
주파수가 5Hz, 10Hz, 20Hz에서 최대값을 가지는데 이는 위에서 설명한 신호 1,2,3 의 주파수임을 알 수 있다. 이건 Original Signal의 Spectrum에서 각 신호들의 frequency의 power가 최대임을 말하는데 메시지 전달 신호에서 Power를 소비하므로 당연한 소리이다.
원래 신호가 이다.
이것의 Spectrum (주파수에 대한 식)을 구하면
식과 그래프와 비교 했을 때, x축의 (-)좌표들이 나오지 않아 Power Spectral Density가 그림에 완전히 표현되어 있지 않다. x축의 (-)좌표들도 그림에 나타내면 위의 그림과 y출 대칭된 그림이 나타날 것이다.
식과 그래프와 비교시, 5Hz의 power 가 최대치인 이유는 S(f)에서 보면 5Hz에서 0.25의 impulse( 제일 큰 값) 을 가지기







































소개글