목차
제목
목적
이론
실험기구
실험방법
결과 Report
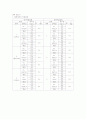
1. 평면에서의 마찰실험
2. 경사면에서의 마찰실험 (각도 : 10˚)
결과 계산
결론
목적
이론
실험기구
실험방법
결과 Report
1. 평면에서의 마찰실험
2. 경사면에서의 마찰실험 (각도 : 10˚)
결과 계산
결론
본문내용
. 코르크
m₁μs = 1.7 - 0.3428*0.17*9.8/0.3428*9.8*0.98 = 0.3
μk = 1.7 - 0.3428*9.8*0.17/0.3428*9.8*0.98 = 0.3
m₂ μs = 3.1*0.5967*9.8*0.17/0.5967*9.8*0.98 = 0.5
μk = 2.6*0.5967*9.8*0.17/0.5967*9.8*0.98 = 0.5
m₃ μs = 4.3*0.8528*9.8*0.17/0.8528*9.8*0.98 = 0.7
μk = 4.0*0.8528*9.8*0.17/0.8528*9.8*0.98 = 0.7
2. 플라스틱
m₁μs = 2.4*05973*0.17*9.8/0.5973*9.8*0.98 = 0.4
μk = 1.8*0.5973*9.8*0.17/0.5973*9.8*0.98 = 0.3
m₂ μs = 2.8*0.8534*9.8*0.17/0.8534*9.8*0.98 = 0.5
μk = 2.4*0.8534*9.8*0.17/0.8534*9.8*0.98 = 0.4
m₃ μs = 4.0*1.1061*9.8*0.17/1.1061*9.8*0.98 = 0.7
μk = 3.8*1.1061*9.8*0.17/1.1061*9.8*0.98 = 0.7
3. 부직포
m₁μs = 2.4*0.5879*0.17*9.8/0.5879*9.8*0.98 = 0.4
μk = 2.0*0.5879*9.8*0.17/0.5879*9.8*0.98 = 0.3
m₂ μs = 3.3*0.8440*9.8*0.17/0.8440*9.8*0.98 = 0.6
μk = 2.8*0.8440*9.8*0.17/0.8440*9.8*0.98 = 0.5
m₃ μs = 4.3*1.0967*9.8*0.17/1.0967*9.8*0.98 = 0.7
μk = 3.5*1.0964*9.8*0.17/1.0964*9.8*0.98 = 0.6
결론
두 물체가 접촉하여 운동할 때, 접촉면을 따라 그 운동을 방해하는 힘을 마찰력이라고 한다. 물체가 다른 물체의 표면에 접하여 움직이려고 할 때 또는 움직이고 있을 때 그 운동을 저지하려는 힘이 접촉면에 따라 작용한다. 이 저항력을 마찰력이라고 한다. 이 힘은 물체의 수직항력과 마찰계수의 곱으로 계산된다.
F = μN (μ : 마찰계수, N = 수직 항력)
마찰계수는 접촉면의 성질에 따라 달라진다. 0보다 크며, 접촉면이 거칠수록 그 값이 1에 가까워진다. 얼음판은 잘 미끄러지므로 마찰계수가 작으며, 아스팔트는 비교적 마찰계수가 크다. 거칠수록(마찰계수가 클수록)커진다. 그리고 이상적인 상태에서 마찰력은 접촉면의 면적에 무관하다.
마찰력의 크기는 수직항력에 비례하는데, 이때의 비례상수가 마찰계수이다. 따라서 같은 수징항력이 작용할 때, 마찰계수가 클수록 마찰력의 크기도 커진다. 마찰력의 크기를 f, 수직항력을 N, 마찰계수를 μ(mu : 뮤)라고 할 때, f = μN의 관계가 성립한다. 마찰의 정도를 나타내는 마찰계수는 물질의 재질, 표면의 매끄러운 정도, 윤활제의 유무와 종류 등에 따라 달라진다. 따라서 마찰 계수는 물질을 구분할 수 있는 상수라고 할 수 없다.
m₁μs = 1.7 - 0.3428*0.17*9.8/0.3428*9.8*0.98 = 0.3
μk = 1.7 - 0.3428*9.8*0.17/0.3428*9.8*0.98 = 0.3
m₂ μs = 3.1*0.5967*9.8*0.17/0.5967*9.8*0.98 = 0.5
μk = 2.6*0.5967*9.8*0.17/0.5967*9.8*0.98 = 0.5
m₃ μs = 4.3*0.8528*9.8*0.17/0.8528*9.8*0.98 = 0.7
μk = 4.0*0.8528*9.8*0.17/0.8528*9.8*0.98 = 0.7
2. 플라스틱
m₁μs = 2.4*05973*0.17*9.8/0.5973*9.8*0.98 = 0.4
μk = 1.8*0.5973*9.8*0.17/0.5973*9.8*0.98 = 0.3
m₂ μs = 2.8*0.8534*9.8*0.17/0.8534*9.8*0.98 = 0.5
μk = 2.4*0.8534*9.8*0.17/0.8534*9.8*0.98 = 0.4
m₃ μs = 4.0*1.1061*9.8*0.17/1.1061*9.8*0.98 = 0.7
μk = 3.8*1.1061*9.8*0.17/1.1061*9.8*0.98 = 0.7
3. 부직포
m₁μs = 2.4*0.5879*0.17*9.8/0.5879*9.8*0.98 = 0.4
μk = 2.0*0.5879*9.8*0.17/0.5879*9.8*0.98 = 0.3
m₂ μs = 3.3*0.8440*9.8*0.17/0.8440*9.8*0.98 = 0.6
μk = 2.8*0.8440*9.8*0.17/0.8440*9.8*0.98 = 0.5
m₃ μs = 4.3*1.0967*9.8*0.17/1.0967*9.8*0.98 = 0.7
μk = 3.5*1.0964*9.8*0.17/1.0964*9.8*0.98 = 0.6
결론
두 물체가 접촉하여 운동할 때, 접촉면을 따라 그 운동을 방해하는 힘을 마찰력이라고 한다. 물체가 다른 물체의 표면에 접하여 움직이려고 할 때 또는 움직이고 있을 때 그 운동을 저지하려는 힘이 접촉면에 따라 작용한다. 이 저항력을 마찰력이라고 한다. 이 힘은 물체의 수직항력과 마찰계수의 곱으로 계산된다.
F = μN (μ : 마찰계수, N = 수직 항력)
마찰계수는 접촉면의 성질에 따라 달라진다. 0보다 크며, 접촉면이 거칠수록 그 값이 1에 가까워진다. 얼음판은 잘 미끄러지므로 마찰계수가 작으며, 아스팔트는 비교적 마찰계수가 크다. 거칠수록(마찰계수가 클수록)커진다. 그리고 이상적인 상태에서 마찰력은 접촉면의 면적에 무관하다.
마찰력의 크기는 수직항력에 비례하는데, 이때의 비례상수가 마찰계수이다. 따라서 같은 수징항력이 작용할 때, 마찰계수가 클수록 마찰력의 크기도 커진다. 마찰력의 크기를 f, 수직항력을 N, 마찰계수를 μ(mu : 뮤)라고 할 때, f = μN의 관계가 성립한다. 마찰의 정도를 나타내는 마찰계수는 물질의 재질, 표면의 매끄러운 정도, 윤활제의 유무와 종류 등에 따라 달라진다. 따라서 마찰 계수는 물질을 구분할 수 있는 상수라고 할 수 없다.



























소개글