기초회로실험 03 - Thevenin의 정리, 태브닝, 때브닝

소개글

기초회로실험 03 - Thevenin의 정리, 태브닝, 때브닝에 대한 보고서 자료입니다.

목차

1. 관련이론
2. 실험결과
3. 결론 및 토의4. 레퍼런스

본문내용

도
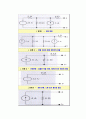
앞에서 구했던 방식으로 를 결정하기 위한 기법이 항상 유용한 가장 쉬운 방법은 아니다. 일반적으로 두 가지의 다른 방법이 사용하기에 더 간단하다. 첫 번째는 회로망이 단지 독립 전원만을 포함하고 있을 때 유용하다. 그런 회로망에 대한 를 계산하기 위해서는 우선 모든 독립 전원을 동작하지 않게 만들고 지정된 단자 쌍에서 망을 바라본 저항을 계한한다. 전압원은 단락 회로로 대체함으로써 동작하지 않게 된다. 전류원은 개방 회로로 대체함으로써 동작하지 않게 된다. 예를 들어 아래 그림의 회로를 생각하자.
독립 전원을 동작하지 않게 힘으로써 오른쪽 위의 그림처럼 회로를 단순화 한다. 단자 a, b에서 바라본 저항은 로 표시 되었고 그것은 과 저항기의 병렬 결합과 직렬인 저항으로 구성 되었다. 따라서 을 구할 수 있다. 앞의 식으로 를 유도하는 것은 앞에서 구했던 것 보다 훨씬 간단하다.
만야에 회로 또는 회로망이 종속 전원을 갖고 있다면 테브냉 저항 를 구하기 위한 다른 처리 과정은 다음과 같다. 우선 모든 독립 전원을 동작시키지 않고, 테브냉 단자 a,b로 테스트 전압원 또는 테스트 전류원 중 하나를 적용한다. 테브냉 저항은 테스트 전원에 의해 유도된 전류에 대한 테스트 전원에 걸린 전압의 비와 같다.
2. 실험 결과
가. 실험1
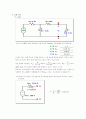
(1),(2) 단자AB에 대한 Thevenin 전압 VTH와 Thevenin 저항 RTH를 계산/측정하라.
계산된 VTH
:
4 V
계산된 RTH
:
11.33 k
측정된 VTH
:
3.99 V
측정된 RTH
:
11.3 k
를 구하기 위해 부하의 연결을 끊는다. 이 때 회로를 만들면 에는 전류가 흐르지
않으므로 전류가 없다. 병렬 연결이므로 의 전압이 와 같다.
전압 분배를 사용하면 , 이므로
AB를 short 시킨 회로를 만들면 아래 방향으로 흐르는 전류가 이다.
회로에서 종속전압원이 없고 독립전원만 있으로 는 독립 전압원을 끄고 저항만 생각해주면 된다. AB에서 바라봤을 때 저항 RTH = 10k + (3.3 || 2.2)= 11.33k이다.
(3) 측정된 등가저항과 등가전압으로 등가회로를 만들고 부하저항에 공급되는 전력을
계산하라.
나. 실험2
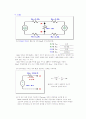
(1),(2) R3를 부하로 했을 때, 저항 RTH를 계산/측정하라.
계산된 VTH
:
0 V
계산된 RTH
:
1.2 k
측정된 VTH
:
0 V
측정된 RTH
:
1.14 k
R3를 부하로 하면 R3에는 전류가 흐르지 않는다고 본다. 위 회로에서는 양쪽에서 같은 전압이 있고 R3에서 같은 전류가 반대로 흘러 상쇄되기 때문에 R3에 흐르는 전류는 없고 전압 'VTH = 0' 이다.
R3를 부하로 보고 AB 사이를 open 시키고 AB에서 바라본 RTH를 구한다.
RTH는 독립전원을 모두 끄고 저항을 합하면 된다. RTH = (2.4k || 2.4k) = 1.2k.
(3) 등가회로를 그리고 부하 R3에 공급되는 전력을 구하여라.
R3에서는 전류가 상쇄되어 흐르지 않으므로 전력은 0이다.
(4) 앞 장의 실험 과정과 비교하여 Thevenin 정리의 편리함을 고려해 볼 것.
Mesh-current를 사용하여 전류값을 계산하면 계산과정도 복잡하고 시간도 오래
소모되며 알아보기도 쉽지 않다. 하지만 Thevenin 정리를 이용하면 아무리 복잡한
회로도 등가회로로 한 눈에 쉽게 알아볼 수 있어서 여러모로 편리하다.
다. 실험3 : Norton의 정리
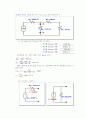
위 회로에 대한 실험값 및 계산값을 기록하라. (R4를 부하로 함)
(1),(2) Norton전류와 Norton저항을 계산/측정.
계산된 Norton 전류
:
2.37 mA
계산된 Norton 저항
:
631.41
측정된 Norton 전류
:
2.370 mA
측정된 Norton 저항
:
631.41
AB를 부하로 하면 AB는 open 되었다고 보고 R4에는 전류가 흐르지 않는다.
그러면 R2에는 전류가 흐르지 않고 VTH = VR3 가 된다.
VTH는 12V의 전압분배를 사용하여 구한다.
RTH는 독립전원을 끄고 저항의 합을 구한다.
(3) 등가회로 그려볼 것.
(4) R3를 부하로 보았을 때, 위의 과정 (1), (2), (3)을 반복해 볼 것.
- 4.1, 4.2) Norton전류와 Norton저항을 계산/측정.
계산된 Norton 전류
:
3.629 mA
계산된 Norton 저항
:
255.17
측정된 Norton 전류
:
3.63 mA
측정된 Norton 저항
:
253.13
독립전원을 끄고 저항의 합을 더하여 RTH를 구한다.
AB가 open되면 R1, R2, R4를 직렬로 보고 전압분배를 사용하여 (R2+R4)에 걸리는 전압을 구한다.
- 4.3) 등가회로 그려볼 것.
3. 결론 및 토의
가. 실험1
종속전원이 없이 독립전원만으로 이루어진 회로에서 RTH를 구할 때는 독립전원을 제거하고 RTH를 구하는 방법이 전원변환이나 다른 방법보다 훨씬 빠르고 쉽게 계산을 할 수 있었다.
나. 실험2
처음에 아무 생각없이 R3에도 전류가 흐를 것이라고 생각하였다. 그래서 R3의 계산치 VTH가 0이 나와서 잘못계산한 줄 알고 Node-Voltage, Mesh-current, KCL 등 여러 가지 방법을 다 동원하여 계산하여보았다. 그 결과는 모두 VTH=0이였다. 반대편에 같은 저항이 연결되어있고 부호가 반대인 전압이 있으므로 같은 전류가 반대로 흘러 R3에는 전류가 흐르지 않아야 한다.
RTH의 측정값이 계산값보다 조금 더 작게 나왔는데 이는 원래 저항기가 약간의 오차를 가지고 있고, 전선도 약간의 저항을 포함하고 있기 때문에 저항 RTH의 측정값이 약간 적게 나온 것 같다.
‘직병렬 회로의 구성 실험’에서 같은 회로를 Mesh-Current 방법을 이용하여 필요한 값들을 구하였고 이번 실험에서는 Thevenin의 정리를 이용하여서 구하였다. Thevenin의 정리를 이용하는 방법이 훨씬더 편하고 빠르고 보기 시간도 더 적게 소모되었다.
다. 실험3
Thevenin과 Norton의 정리를 비교해보면 전원변환으로 서로 쉽게 바꿀 수 있음을 알수 있다.
4. 레퍼런스
- 회로이론/James W.Nilsson/한티미디어/p 153～159

키워드

기초회로실험,   thevenin,   태브닝,   테브냉 등가 유도,   테브냉,   노턴 등가