본문내용
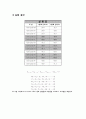
-4 2 1 0 0 0
1 -4 0 1 0 0
1 0 -4 2 1 0
0 1 1 -4 0 1
0 0 1 0 -4 2
0 0 0 1 1 -4
ans =
-0.3304 -0.1964 -0.1250 -0.1250 -0.0446 -0.0536
-0.0982 -0.3304 -0.0625 -0.1250 -0.0268 -0.0446
-0.1250 -0.1250 -0.3750 -0.2500 -0.1250 -0.1250
-0.0625 -0.1250 -0.1250 -0.3750 -0.0625 -0.1250
-0.0446 -0.0536 -0.1250 -0.1250 -0.3304 -0.1964
-0.0268 -0.0446 -0.0625 -0.1250 -0.0982 -0.3304
B =
-42.6000
-86.6000
0
-50.3000
-71.1000
-127.3000
ans =
47.3652
46.6679
53.5250
52.7062
61.3223
60.3321
4) 실험에 대한 고찰
이번 2차원 열전도 실험은 과정은 매우 간단하였지만, 결과값을 도출하는데 매우 애를 먹었다. 위의 실험 결과 데이터를 보게 되면 총 두 단계로 실험을 나눠서 하였는데, 히터의 세기를 1단계와, 3단계로 두고 각각 실험을 하였다. 시편을 히터로 1시간 가열 후 컴퓨터에 연결된 온도 센서를 이용하여 9개의 그리드 점을 빠른시간내에 측정할 계획이었으나, 장비를 사용할 수 없어 한 점씩 각각 접촉시켜 온도를 측정하는 방식을 사용하게 되었다. 이 때문에 각 점마다 오차가 크게 발생하게 되었는데, 그 이유는 완전히 정상상태인지 모르는 상태에서 한점을 측정 후 다음 점으로 이동하게되는 시간동안 시편은 계속 해서 가열이 되고 있었기 때문이다. 이 때문에 조교님께서는 미리 실험 전에 사전실험을 통하여 오차를 줄일 수 있는 방법을 고안하셨다. B-A-C-2-1-D-4-3-E--6-5-F-G 순으로 그리드 점의 온도를 측정하게되면 윗면에 있을수록 열전도가 아무래도 적을 것이고, 가장 낮은 점의 온도를 측정하고 그다음은 조금 더 높은 온도를 측정하게 되어 온도측정기의 접촉면이 식는데 까지 기다리는데서 오는 오차를 잡을 수 있기 때문이다.
하지만 또 다른 오차를 발생하는 요인이 있었다. 가정에서는 3면이 등온상태이고 히터와 접촉하는 면만 가열되어 정상상태에 이른다고 말하고 있지만, 3면을 등온상태로 만들기란 여간쉬운일이 아니다. 조교님께서 고안해 내신 세라믹 방열판으로 3면을 둘러쌌고, 히터판에서 시편으로 바로 전도되는 열 이외에 공기를 통하여 열이 전도되는 것도 막기위하여 히터와 시편의 접촉면을 제외한 히터판을 방열판으로 막았다.
크게 오차를 발생시키는 위의 두가지 요인을 조교님의 사전 실험을 통하여 보안하므로써 실험 결과 데이터에서 보는 것과 같이 오차율은 3%미만을 기록하면 거의 정확한 실험 값을 얻을 수 있었다.
정확한 실험을 한 후 부터는 이차원 정상 상태 열 전도 방정식을 통하여 실험값을 도출하는데 큰 애를 먹었다. MATLAB을 통하여 먼저 이론값을 도출하는데는 큰 어려움이 없었지만 , 가우스 소거법을 이용하여 직접 미지수값을 도출하는데 계속하여 잘 못된 계산이 되어 큰애를 먹었다. 를 이용하여 A~G까지 실험값을 상수로 넣고, 을 미지수로 넣으면 총 6개의 미지수와 6개의 방정식이 나온다.
이를 MATRIX형태로 나타내면 형태가 된다.
1단계와 3단계로 변화시키면서 실험한 데이터값을 넣고 가우스 소거법을 사용하면 값이 나오게 된다.
기계공학실험 첫 실험 보고서를 쓰면서 많은 난관에 봉착했지만, 심혈을 기울여 여러 가지 난관을 넘어서기 위해 MATLAB, 행렬식을 공부하게 되어 매우 유익한 실험이 되었다.
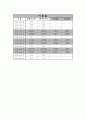
1 -4 0 1 0 0
1 0 -4 2 1 0
0 1 1 -4 0 1
0 0 1 0 -4 2
0 0 0 1 1 -4
ans =
-0.3304 -0.1964 -0.1250 -0.1250 -0.0446 -0.0536
-0.0982 -0.3304 -0.0625 -0.1250 -0.0268 -0.0446
-0.1250 -0.1250 -0.3750 -0.2500 -0.1250 -0.1250
-0.0625 -0.1250 -0.1250 -0.3750 -0.0625 -0.1250
-0.0446 -0.0536 -0.1250 -0.1250 -0.3304 -0.1964
-0.0268 -0.0446 -0.0625 -0.1250 -0.0982 -0.3304
B =
-42.6000
-86.6000
0
-50.3000
-71.1000
-127.3000
ans =
47.3652
46.6679
53.5250
52.7062
61.3223
60.3321
4) 실험에 대한 고찰
이번 2차원 열전도 실험은 과정은 매우 간단하였지만, 결과값을 도출하는데 매우 애를 먹었다. 위의 실험 결과 데이터를 보게 되면 총 두 단계로 실험을 나눠서 하였는데, 히터의 세기를 1단계와, 3단계로 두고 각각 실험을 하였다. 시편을 히터로 1시간 가열 후 컴퓨터에 연결된 온도 센서를 이용하여 9개의 그리드 점을 빠른시간내에 측정할 계획이었으나, 장비를 사용할 수 없어 한 점씩 각각 접촉시켜 온도를 측정하는 방식을 사용하게 되었다. 이 때문에 각 점마다 오차가 크게 발생하게 되었는데, 그 이유는 완전히 정상상태인지 모르는 상태에서 한점을 측정 후 다음 점으로 이동하게되는 시간동안 시편은 계속 해서 가열이 되고 있었기 때문이다. 이 때문에 조교님께서는 미리 실험 전에 사전실험을 통하여 오차를 줄일 수 있는 방법을 고안하셨다. B-A-C-2-1-D-4-3-E--6-5-F-G 순으로 그리드 점의 온도를 측정하게되면 윗면에 있을수록 열전도가 아무래도 적을 것이고, 가장 낮은 점의 온도를 측정하고 그다음은 조금 더 높은 온도를 측정하게 되어 온도측정기의 접촉면이 식는데 까지 기다리는데서 오는 오차를 잡을 수 있기 때문이다.
하지만 또 다른 오차를 발생하는 요인이 있었다. 가정에서는 3면이 등온상태이고 히터와 접촉하는 면만 가열되어 정상상태에 이른다고 말하고 있지만, 3면을 등온상태로 만들기란 여간쉬운일이 아니다. 조교님께서 고안해 내신 세라믹 방열판으로 3면을 둘러쌌고, 히터판에서 시편으로 바로 전도되는 열 이외에 공기를 통하여 열이 전도되는 것도 막기위하여 히터와 시편의 접촉면을 제외한 히터판을 방열판으로 막았다.
크게 오차를 발생시키는 위의 두가지 요인을 조교님의 사전 실험을 통하여 보안하므로써 실험 결과 데이터에서 보는 것과 같이 오차율은 3%미만을 기록하면 거의 정확한 실험 값을 얻을 수 있었다.
정확한 실험을 한 후 부터는 이차원 정상 상태 열 전도 방정식을 통하여 실험값을 도출하는데 큰 애를 먹었다. MATLAB을 통하여 먼저 이론값을 도출하는데는 큰 어려움이 없었지만 , 가우스 소거법을 이용하여 직접 미지수값을 도출하는데 계속하여 잘 못된 계산이 되어 큰애를 먹었다. 를 이용하여 A~G까지 실험값을 상수로 넣고, 을 미지수로 넣으면 총 6개의 미지수와 6개의 방정식이 나온다.
이를 MATRIX형태로 나타내면 형태가 된다.
1단계와 3단계로 변화시키면서 실험한 데이터값을 넣고 가우스 소거법을 사용하면 값이 나오게 된다.
기계공학실험 첫 실험 보고서를 쓰면서 많은 난관에 봉착했지만, 심혈을 기울여 여러 가지 난관을 넘어서기 위해 MATLAB, 행렬식을 공부하게 되어 매우 유익한 실험이 되었다.


























소개글