목차
Ⅰ. AES(Advanced Encryption Standard)
1. 개요
□ 정의
□ 특징
□ 설계적 특징
2. AES의 구조
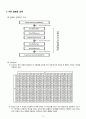
□ 전체적 구조
3. AES 암호화 과정
□ 암호화 전체적인 구조
□ SubBytes
□ ShiftRows
□ MixColumns
□ AddRoundKey
4. AES 복호화 과정
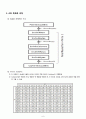
□ 복호화 전체적인 구조
□ Inverse SubBytes
□ Inverse ShiftRows
□ Inverse MixColumns
□ Inverse AddRoundKey
Ⅱ. RSA( Rivest Shamir Adleman )
1. 개요
□ 정의
□ 특징
2. RSA의 구조
□ 전체 과정
3. RSA 암호화, 복호화
□ 전체 과정 표
□ 복호화 과정 확인
Ⅲ. AES(관용 암호) 와 RSA(공개키 암호) 비교
□ 비교 표
1. 개요
□ 정의
□ 특징
□ 설계적 특징
2. AES의 구조
□ 전체적 구조
3. AES 암호화 과정
□ 암호화 전체적인 구조
□ SubBytes
□ ShiftRows
□ MixColumns
□ AddRoundKey
4. AES 복호화 과정
□ 복호화 전체적인 구조
□ Inverse SubBytes
□ Inverse ShiftRows
□ Inverse MixColumns
□ Inverse AddRoundKey
Ⅱ. RSA( Rivest Shamir Adleman )
1. 개요
□ 정의
□ 특징
2. RSA의 구조
□ 전체 과정
3. RSA 암호화, 복호화
□ 전체 과정 표
□ 복호화 과정 확인
Ⅲ. AES(관용 암호) 와 RSA(공개키 암호) 비교
□ 비교 표
본문내용
사용하며 상태 배열의 각 바이트에서 왼쪽 4비트는 행 값, 오른쪽 4비트는 열값으로 사용됨
이 행과 열값을 인덱스로 이용하여 S-Box에서 유일한 8비트 출력 값을 선택함(예를 들어 16진수 {89}는 S-Box에서 8행, 9열에 해당하며, 그 값은 {A7}이므로 상태 배열의 값 {89}는 {A7}로 치환됨
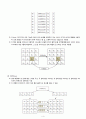
ShiftRows
상태 배열에서 첫 번째 행은 그대로 두고, 두 번째 행은 1바이트, 세 번째 행은 2바이트, 네 번째 행은 3바이트씩 왼쪽으로 순환이동 시킴
이 변환은 4바이트가 4개의 다른 열로 흩어지는 효과를 얻을 수 있음
아래는 ShiftRows의 예
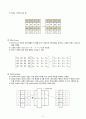
MixColumns
MixColumns 연산은 상태 배열의 각 열을 GF() 상에서의 다항식들로 생각하고, 고정된 다항식 c(x)와 곱셈을 수행함
고정된 다항식 c(x)는 c(x) = 03 * +++02로 계산됨
따라서 아래와 같은 곱셈 행태로 나타낼 수 있음
AddRoundKey
AddRoundKey 연산은 라운드 키와 현재 State를 비트 단위로 XOR를 수행하는 과정임
암호화 과정의 State와 라운드 키는 동일한 크기를 가지며, 1라운드를 수행하기 전에 초기 평문과 라운드 키를 XOR하는 과정이 필요하므로, AddRoundKey 연산은 전체 암호화 과정에서 Nr+1번 수행하게 됨
현재 State와 라운드 키의 AddRoundKey 연산과정은 아래와 같음
4. AES 복호화 과정
복호화 전체적인 구조
Inverse SubBytes
이 과정은 S-Box를 이용한 바이트 단위의 치환 연산인 SubBytes의 역변환임
SubBytes에서 적용한 Afine 변환의 역 변환을 적용한 후, 각 바이트 단위로 GF()상의 곱셈의 역을 취하여 구할 수 있음
Inverse SubBytes에서 수행되는 변환을 행렬 형태로 표현하면 아래와 같음
Inverse ShiftRows
첫 번째 행은 그대로 두고, 두 번째 행은 1바이트, 세 번째 행은 2바이트, 네 번째 행은 3바이트 오른쪽으로 순환이동 시킴
아래는 InvShiftRows의 예
Inverse MixColumns
MixColumns의 역 과정으로 다항식 c(x와 곱셈을 수행함
c(x은 c(x) = {0B} + {0D} + {09}x + {0E}로 계산됨
Inverse AddRoundKey
어떤 값에 XOR 연산을 취하고 동일한 값을 다시 XOR 연산하면 원래의 값이 복원되기 때문에 역 라운드 키 추가 변환은 순 라운드 키 추가 변환과 동일하게 수행함
Ⅱ. RSA( Rivest Shamir Adleman )
1. 개요
정의
공개키 암호화시스템으로, 암호화 뿐 아니라 전자서명이 가능한 최초의 알고리즘으로 알려져 있다.
RSA는 소인수분해의 난해함에 기반을 두어, 공개키만을 가지고는 개인키를 쉽게 짐작할 수 없다.
1977년 로널드 라이베스트(Ron Rivest), 아디 샤미르(Adi Shamir), 레오널드 애들먼(Leonard Adleman)의 연구에 의해 체계화되었으며 RSA라는 이름은 이들 3명의 이름 앞글자를 딴 것이다.
암호화 할 때 쓰는 키와 복호화 할 때 쓰는 키가 다른 비대칭형 암호 방식의 일종이다.
특징
암호 열쇠와 복호 열쇠가 다르다.
암호 열쇠가 있어도 복호가 되지 않는다.
공개되어 있으므로 상대에게 넘길 필요가 없다.
2. RSA의 구조
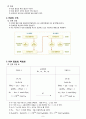
전체 과정
B에게 평문 M을 비밀리에 전달하려는 A는 공개목록에서 B의 공개키를 찾는다.
암호문을 계산하여 B에게 전송한다.
B는 A로부터 수신한 암호문을 자신이 보관하고 있는 개인키로 평문으로 복원한다.
3. RSA 암호화, 복호화
전체 과정 표
가입자 A
공개목록
KeA , nA , KeB , nB
가입자 B
pA , qA
nA=pA· qA
0(nA) = (pA 1)(qA 1)
gcd(KeA , 0(nA)) = 1
KeA · KdA≡ 1 mod 0(nA)
C ≡ MKeB mod nB
C
pB , qB
nB=pB· qB
0(nB) = (pB 1)(qB 1)
gcd(KeB , 0(nB)) = 1
KeB· KdB≡ 1 mod 0(nB)
M ≡ CKdB mod nB
두 개의 서로 다른 큰 소수를 선택한다. 이를 각각 p , q 라고 하자
두 개의 소수 p , q를 곱하여 새로운 수 n을 계산한다 즉, n = p*q 라 한다.
(p-1) * (q-1)와 서로소 이고 n 보다는 작은 Ke 를 구한다.
KeA · KdA≡ 1 mod 0(nA) 식을 이용해 Kd 를 구한다.
Ke(공개키) , Kd(개인키) , C ≡ MKeB mod nB(암호화) , M ≡ CKdB mod nB(복호화)
복호화 과정 확인
Ke(공개키) 와 Kd(개인키) 가 mod 0(n)상에서 서로 역수 관계가 있으므로
Ke · Kd ≡ 1 mod 0(n)
임의의 t에 관하여
Ke · Kd = t0(n)+1 이 성립한다.
암호문 C ≡ MKe mod n이므로 복호화 과정을 적용하면 다음 식이 성립한다. (gcd(M,n) = 1 이라 가정)
CKd ≡ (MKe)Kd mod n
≡ MKeKd mod n
≡ Mt0(n)+1 mod n
≡ Mt0(n) · M mod n
≡ (M0(n))t · M mod n
≡ 1t · M mod n
≡ M mod n
위 식에서 알 수 있듯이 개인키 Kd 로 암호문 C로부터 평문 M을 복원 할 수 있다.
Ⅲ. AES(관용 암호) 와 RSA(공개키 암호) 비교
비교 표
비교 항목
관용 암호화
공개키 암호화
키 개수
한 개의 키를 사용
두 개의 키를 사용
키 보관 형태
비밀리에 보관
개인키는 비밀리, 공개키는 어디든지 배포
키 교환
어려우며 위험하다
공개키를 교환하는 것은 매우 쉽다
키 길이
64비트, 128비트 등 작은 길이
512,1024,2048비트 등 큰 길이
암호화 속도
빠르다
느리다
암호화할 수 있는 평문의 길이
제한 없음
제한 있음
기밀성
가능함
가능함
인증
부분적 가능함
가능함
무결성
부분적 가능함
가능함
부인 방지
불가능
가능함
예를 들어 공개키 같은 경우는 은행의 인터넷뱅킹 결재시나 24시간 현금 인출기의 비밀번호나 기타 정보와 전산망의 자료를 주고 받을 때 사용되고 있고, 여러 분야에서 각각의 장·단점에
이 행과 열값을 인덱스로 이용하여 S-Box에서 유일한 8비트 출력 값을 선택함(예를 들어 16진수 {89}는 S-Box에서 8행, 9열에 해당하며, 그 값은 {A7}이므로 상태 배열의 값 {89}는 {A7}로 치환됨
ShiftRows
상태 배열에서 첫 번째 행은 그대로 두고, 두 번째 행은 1바이트, 세 번째 행은 2바이트, 네 번째 행은 3바이트씩 왼쪽으로 순환이동 시킴
이 변환은 4바이트가 4개의 다른 열로 흩어지는 효과를 얻을 수 있음
아래는 ShiftRows의 예
MixColumns
MixColumns 연산은 상태 배열의 각 열을 GF() 상에서의 다항식들로 생각하고, 고정된 다항식 c(x)와 곱셈을 수행함
고정된 다항식 c(x)는 c(x) = 03 * +++02로 계산됨
따라서 아래와 같은 곱셈 행태로 나타낼 수 있음
AddRoundKey
AddRoundKey 연산은 라운드 키와 현재 State를 비트 단위로 XOR를 수행하는 과정임
암호화 과정의 State와 라운드 키는 동일한 크기를 가지며, 1라운드를 수행하기 전에 초기 평문과 라운드 키를 XOR하는 과정이 필요하므로, AddRoundKey 연산은 전체 암호화 과정에서 Nr+1번 수행하게 됨
현재 State와 라운드 키의 AddRoundKey 연산과정은 아래와 같음
4. AES 복호화 과정
복호화 전체적인 구조
Inverse SubBytes
이 과정은 S-Box를 이용한 바이트 단위의 치환 연산인 SubBytes의 역변환임
SubBytes에서 적용한 Afine 변환의 역 변환을 적용한 후, 각 바이트 단위로 GF()상의 곱셈의 역을 취하여 구할 수 있음
Inverse SubBytes에서 수행되는 변환을 행렬 형태로 표현하면 아래와 같음
Inverse ShiftRows
첫 번째 행은 그대로 두고, 두 번째 행은 1바이트, 세 번째 행은 2바이트, 네 번째 행은 3바이트 오른쪽으로 순환이동 시킴
아래는 InvShiftRows의 예
Inverse MixColumns
MixColumns의 역 과정으로 다항식 c(x와 곱셈을 수행함
c(x은 c(x) = {0B} + {0D} + {09}x + {0E}로 계산됨
Inverse AddRoundKey
어떤 값에 XOR 연산을 취하고 동일한 값을 다시 XOR 연산하면 원래의 값이 복원되기 때문에 역 라운드 키 추가 변환은 순 라운드 키 추가 변환과 동일하게 수행함
Ⅱ. RSA( Rivest Shamir Adleman )
1. 개요
정의
공개키 암호화시스템으로, 암호화 뿐 아니라 전자서명이 가능한 최초의 알고리즘으로 알려져 있다.
RSA는 소인수분해의 난해함에 기반을 두어, 공개키만을 가지고는 개인키를 쉽게 짐작할 수 없다.
1977년 로널드 라이베스트(Ron Rivest), 아디 샤미르(Adi Shamir), 레오널드 애들먼(Leonard Adleman)의 연구에 의해 체계화되었으며 RSA라는 이름은 이들 3명의 이름 앞글자를 딴 것이다.
암호화 할 때 쓰는 키와 복호화 할 때 쓰는 키가 다른 비대칭형 암호 방식의 일종이다.
특징
암호 열쇠와 복호 열쇠가 다르다.
암호 열쇠가 있어도 복호가 되지 않는다.
공개되어 있으므로 상대에게 넘길 필요가 없다.
2. RSA의 구조
전체 과정
B에게 평문 M을 비밀리에 전달하려는 A는 공개목록에서 B의 공개키를 찾는다.
암호문을 계산하여 B에게 전송한다.
B는 A로부터 수신한 암호문을 자신이 보관하고 있는 개인키로 평문으로 복원한다.
3. RSA 암호화, 복호화
전체 과정 표
가입자 A
공개목록
KeA , nA , KeB , nB
가입자 B
pA , qA
nA=pA· qA
0(nA) = (pA 1)(qA 1)
gcd(KeA , 0(nA)) = 1
KeA · KdA≡ 1 mod 0(nA)
C ≡ MKeB mod nB
C
pB , qB
nB=pB· qB
0(nB) = (pB 1)(qB 1)
gcd(KeB , 0(nB)) = 1
KeB· KdB≡ 1 mod 0(nB)
M ≡ CKdB mod nB
두 개의 서로 다른 큰 소수를 선택한다. 이를 각각 p , q 라고 하자
두 개의 소수 p , q를 곱하여 새로운 수 n을 계산한다 즉, n = p*q 라 한다.
(p-1) * (q-1)와 서로소 이고 n 보다는 작은 Ke 를 구한다.
KeA · KdA≡ 1 mod 0(nA) 식을 이용해 Kd 를 구한다.
Ke(공개키) , Kd(개인키) , C ≡ MKeB mod nB(암호화) , M ≡ CKdB mod nB(복호화)
복호화 과정 확인
Ke(공개키) 와 Kd(개인키) 가 mod 0(n)상에서 서로 역수 관계가 있으므로
Ke · Kd ≡ 1 mod 0(n)
임의의 t에 관하여
Ke · Kd = t0(n)+1 이 성립한다.
암호문 C ≡ MKe mod n이므로 복호화 과정을 적용하면 다음 식이 성립한다. (gcd(M,n) = 1 이라 가정)
CKd ≡ (MKe)Kd mod n
≡ MKeKd mod n
≡ Mt0(n)+1 mod n
≡ Mt0(n) · M mod n
≡ (M0(n))t · M mod n
≡ 1t · M mod n
≡ M mod n
위 식에서 알 수 있듯이 개인키 Kd 로 암호문 C로부터 평문 M을 복원 할 수 있다.
Ⅲ. AES(관용 암호) 와 RSA(공개키 암호) 비교
비교 표
비교 항목
관용 암호화
공개키 암호화
키 개수
한 개의 키를 사용
두 개의 키를 사용
키 보관 형태
비밀리에 보관
개인키는 비밀리, 공개키는 어디든지 배포
키 교환
어려우며 위험하다
공개키를 교환하는 것은 매우 쉽다
키 길이
64비트, 128비트 등 작은 길이
512,1024,2048비트 등 큰 길이
암호화 속도
빠르다
느리다
암호화할 수 있는 평문의 길이
제한 없음
제한 있음
기밀성
가능함
가능함
인증
부분적 가능함
가능함
무결성
부분적 가능함
가능함
부인 방지
불가능
가능함
예를 들어 공개키 같은 경우는 은행의 인터넷뱅킹 결재시나 24시간 현금 인출기의 비밀번호나 기타 정보와 전산망의 자료를 주고 받을 때 사용되고 있고, 여러 분야에서 각각의 장·단점에
키워드
추천자료
 전자상거래의 보안문제
전자상거래의 보안문제 [자연과학] RNA (Ribo Nucleic Acid)
[자연과학] RNA (Ribo Nucleic Acid) DEA를 통한 정보보안의 상대적 효율성측정-서울시 기초자치단체를 중심으로-
DEA를 통한 정보보안의 상대적 효율성측정-서울시 기초자치단체를 중심으로- 디지털 텔레비전의 미래, MHP
디지털 텔레비전의 미래, MHP IPV4와 IPV6의 비교(2007년 최신자료)
IPV4와 IPV6의 비교(2007년 최신자료) [저작권][저작권보호]다양한 사례와 판례를 통해 본 저작권의 실태와 저작권보호의 필요성 및...
[저작권][저작권보호]다양한 사례와 판례를 통해 본 저작권의 실태와 저작권보호의 필요성 및... [해커][시스템침입][해킹][시스템보안]해커의 시스템침입(해킹) 과정과 해커의 시스템침입(해...
[해커][시스템침입][해킹][시스템보안]해커의 시스템침입(해킹) 과정과 해커의 시스템침입(해... [방화벽][방화벽시스템][방화벽시스템 주요기능][방화벽시스템 유형][방화벽시스템구축][보안...
[방화벽][방화벽시스템][방화벽시스템 주요기능][방화벽시스템 유형][방화벽시스템구축][보안... [전자화폐][한국 전자화폐][외국 전자화폐][지불결제수단]전자화폐의 분류, 전자화폐의 거래,...
[전자화폐][한국 전자화폐][외국 전자화폐][지불결제수단]전자화폐의 분류, 전자화폐의 거래,... 2011년 하계계절시험 멀티미디어시스템 시험범위 핵심체크
2011년 하계계절시험 멀티미디어시스템 시험범위 핵심체크 2011년 2학기 멀티미디어시스템 기말시험 핵심체크
2011년 2학기 멀티미디어시스템 기말시험 핵심체크 컴퓨터 보안과 활용
컴퓨터 보안과 활용 [불건전정보]불건전정보유통의 청소년의식조사, 불건전정보유통의 차단기술, 불건전정보유통...
[불건전정보]불건전정보유통의 청소년의식조사, 불건전정보유통의 차단기술, 불건전정보유통... 기업 EC(전자상거래)의 의미, 분류, 기업 EC(전자상거래)의 특징, 기업 EC(전자상거래)의 구...
기업 EC(전자상거래)의 의미, 분류, 기업 EC(전자상거래)의 특징, 기업 EC(전자상거래)의 구...


























소개글