|
변환이다.
탐사의 목적이 불발탐과 같은 지하의 자성물체를 탐사하는 경우에는 그해석이 매우 직접적이다. 즉 강한 이상이 있는 곳에 이상 물질이 있다. 이 경우에는 잡음의 제거, 잔여 이상의 분리 및 향상이 매우 중요하다. 잡음의 공간적
|
|
|
푸리에 급수를 이용한 차동형 신호의 경제적인 저장법, 한국비파괴검사학회, 2002
이석우 외 2명, 음성신호의 스펙트로그램 분석 시스템 구현, 대한전자공학회, 1990
이현철, 수동적 전기특성을 이용한 인체의 신호전달방향 계측법 개발, 원광
|
|
|
1번) Conplex translation 정리를 이용하여 다음 함수의 라플라스 변환을 구하여라.
f(t)=
=> coswt= , sinwt= 이므로
F(s)={A (coswtcos -sinwtsin)}
={A(coswtcos)} -{A(sinwtsin)}
=Acos[coswt]-Asin[sinwt]
ⅰ) coswt=f(t) 로 놓으면
[f(t)]=F(s+) 인데
F(s)=이므로
F(s+)=
즉 Acos[coswt] =
|
|
|
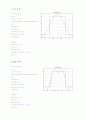
for k=-19:1:19;
y=y+5*sinc(1/2*k)*cos(pi/2*k*t);
end
x(t<0)=0;
x(t>0)=1;
x1=10*(t+1>=0);
x2=-10*(t-1>=0);
x=x1+x2;
figure
plot(t,y,\'r\');
hold on
plot(t,x);
title(\'푸리에급수 N=19\');
grid on
5.N=79 일 때
t=-2:0.01:2;
y=0;
for k=-79:1:79;
y=y+5*sinc(1/2*k)*cos(pi/2*k*t);
end
x(t<0)=
|
|
|
공학수학 라플라스변환 핵심요약정리비법노트A+시험 및 전공면접 대비용
|
|
|
안정도를 결정할 수 있는 방법을 개발 ( 나이퀴스트 선도, 보드선도)
- 궤환(feedback)제어 시스템의 특성 방정식을 그림으로 푸는 방법이 개발(근궤적; root locus) 1.자동제어 역사와 종류 및 필요성
2.PID제어
3.라플라스 변환
|
|
|
푸리에 급수란?
-프랑스 수학자 푸리에⇒임의의 주기함수는 사인과 코사인의 무한급수로 전개됨을 최초 증명
- 직교좌표계에 의한 함수의 급수 전개. 임의의 주기함수를 삼각함수로 구성되는 급수로 전개한 것을 말한다.
- 푸리에 급수에서
|
|
|
연산으로 보조방정식 풀이
ⅲ) 보조방정식의 해를 역으로 변환- 역변환
라플라스 변환이란 무엇이며, 라플라스 변환의 목적은 어디에 있고, 응용에 관련된 분야
에 대해서.,..
1. 불연속인 함수의 라플라스 변환은 연속함수가 되어 표현이 하
|
|
|
푸리에 급수
푸리에 급수는 주기 함수를 삼각함수의 가중치로 분해하여 해석하는 수학적 기법이다. 가중치, 또는 계수는 본래 함수와 일대일 대응한다. 일반 푸리에 급수는 직교 기저에서 전개한다.
푸리에 급수에서의 계수는 본래 함수보다
|
|
|
라플라스변환하였을 경우 아래와 같은 식이 완성됨
-시간이동(time shift)를 하였을 경우 다음과 같이 표현. T초만큼 이동함을 표현
이를 라플라스 변환하였을 경우 다음과 같은 식이 완성됨
-회로의 응답특성: 콘볼루션(합성곱) 이것은 하나의
|
|
메뉴펼치기
