목차
1. Preknowledge
1-1. 본 실험에서의 레이놀즈 수
1-2. NACA0012 Airfoil의 형상과 압력탭의 좌표값
* 형상
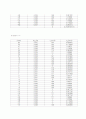
* 압력탭의 좌표값
2-1. 3가지 받음각에 대한 에어포일의 압력 값 측정
1) 받음각이 0도일 때
2) 받음각이 7도일 때
3) 받음각이 -7도일 때
2-2. 각각의 받음각에 대한 압력계수와 플롯
* 각각의 받음각에 대한 압력계수
* 각각의 받음각에 대한 압력계수 플롯
1) 각각의 각도 및 좌표에서의 윗 부분 압력계수
2) 각각의 각도 및 좌표에서의 아랫 부분 압력계수
3) 각 각의 각도에서 위, 아래 부분의 압력계수 플롯
2-3. 3가지 받음각에 대한 후류 속도 값 측정
* 받음각 0도를 기준으로 보정된 결과 값
* 각각의 받음각에 대한 에어포일의 후류속도
* 각각의 받음각에 대한 에어포일의 후류속도 plot (by MATLAB)
1) 받음각 0°
2) 받음각 7°
3) 받음각 -7°
2-4. 최종결과
1) 압력을 이용한 항력계수, 양력계수, 항력, 양력 값
1) 받음각 0°
2) 받음각 7°
3) 받음각 -7°
2) 후류속도를 이용한 항력계수 및 항력 값
1) 받음각 0°
2) 받음각 7°
3) 받음각 -7°
3. Data Analysis
3.1 2.4 최종결과 데이터의 분석
3.2 얇은 익형 이론을 통한 결과와의 비교
3.3 참고문헌을 통한 값과의 비교와 타당성 검증
4. Reference
1-1. 본 실험에서의 레이놀즈 수
1-2. NACA0012 Airfoil의 형상과 압력탭의 좌표값
* 형상
* 압력탭의 좌표값
2-1. 3가지 받음각에 대한 에어포일의 압력 값 측정
1) 받음각이 0도일 때
2) 받음각이 7도일 때
3) 받음각이 -7도일 때
2-2. 각각의 받음각에 대한 압력계수와 플롯
* 각각의 받음각에 대한 압력계수
* 각각의 받음각에 대한 압력계수 플롯
1) 각각의 각도 및 좌표에서의 윗 부분 압력계수
2) 각각의 각도 및 좌표에서의 아랫 부분 압력계수
3) 각 각의 각도에서 위, 아래 부분의 압력계수 플롯
2-3. 3가지 받음각에 대한 후류 속도 값 측정
* 받음각 0도를 기준으로 보정된 결과 값
* 각각의 받음각에 대한 에어포일의 후류속도
* 각각의 받음각에 대한 에어포일의 후류속도 plot (by MATLAB)
1) 받음각 0°
2) 받음각 7°
3) 받음각 -7°
2-4. 최종결과
1) 압력을 이용한 항력계수, 양력계수, 항력, 양력 값
1) 받음각 0°
2) 받음각 7°
3) 받음각 -7°
2) 후류속도를 이용한 항력계수 및 항력 값
1) 받음각 0°
2) 받음각 7°
3) 받음각 -7°
3. Data Analysis
3.1 2.4 최종결과 데이터의 분석
3.2 얇은 익형 이론을 통한 결과와의 비교
3.3 참고문헌을 통한 값과의 비교와 타당성 검증
4. Reference
본문내용
따른 camber line의 함수이다. 하지만 NACA0012의 geometry의 성질 상 Camber line은 ‘0’으로 나온다. 하지만 우선 이를 고려하여 일반적으로 식을 전개하자.
angle of attack의 값과 airfoil의 geometry에 따라
이 때 airfoil의 형상을 살펴볼 때 thickness가 chord의 최대 12%이기 때문에 tangent를 근사시킬 수 있다.
따라서 우선 Free stream의 foil에 대한 수직성분은
가 된다.
두 번째로 살펴볼 값은 vortex로 발생하는 속도성분의 분석이다. chord line의 각 지점에 분포한 vortex에 의해 camber line위의 임의의 위치 x에 발생하는 수직속도를 라 할 때, airfoil의 camber line을 chord line으로 근사시킬 수 있으며
의 관계를 비로소 만족하게 된다.
미소 chord line 위의 vortex에 의한 수직속력의 미소성분은 다음과 같으며 이를 전 chord line에 대하여 적분을 한 값이 첫 번째로 구한 free stream의 foil 에 대한 수직속도와 같아야 한다.
--
이 때 NACA0012에 대하여 수식을 전개할 때 이 airfoil 은 대칭적인 형상이므로 camber line이 chord line이 일치하며 이 만족된다.
이 때 chord line 위의 원점으로부터의 길이를 (r,θ) coordinate로 변환하여 전개하면 (이 때 r의 중심은 chord line의 절반인 지점이다.)
의 관계가 얻어져 이를 준식에 적용하면
이 된다.
이를 Fourier transform을 이용하여 구하면 다음과 같다.
이는 아래의 증명에 의해 Kutta condition까지 만족시키는 것임을 알 수 있다.
이를 이용하여 chord line 전체의 circulation을 구하면
과 같고 Kutta-Koukowski theorem에 따라
이므로 이때의 lift coefficient를 구하면
이 된다.
-그림 참조- John D.Anderson. Jr, Fundamental of Aerodynamics 4th edition, p.326 McGrawHill
* 얇은 익형 이론을 이용한 항력
d\'Alembert\'s paradox
유체가 inviscid flow라고 가정했을 때,
∞를 free stream에 대한 첨자, s를 surface의 첨자라 하고
Bernoulli\'s equatinon에 의하면,
or ―(1)
여기서, 이고, 가 cylinder의 depth라고 하자.
(1)에서 유도된 를 위 식에 대입하여 적분을 하면, 에 대한 term에 의하여
(cylinder with circulation) = 0
이것이 d\'Alembert\'s paradox이다.
inviscid theory에 따르면, 유체의 free stream(uniform stream)에 잠겨 있는 어떠한 모양의 물체의 drag는 항상 0이다.
실제실험이 inviscid 상태가 아니기 때문에 inviscid 상태를 가정한 ‘얇은 익형 이론’ 을 적용할 수 없다. 따라서 우리는 상용프로그램에서 Cd 값을 구하여 분석해 보았다.
* 얇은 익형 이론을 이용한 값과 실험값과의 비교(두 가지 방법을 통한 값 모두 비교)
이론값
Cp 분포를 통한 실험값
Cl오차율(%)
후류속도를 통한 실험값
AOA(deg)
Cl
Cd
Cl
Cd
/
Cd
0
0
0
0
0.035896
/
/
0.162853
7
0.767636
0
0.690077
0.08459
10.1036
/
0.167009
-7
-0.76764
0
-0.60209
0.029416
21.56568
/
0.15822
위에서 정리하였듯이 이론값에 의하여 thin airfoil theory에서 lift coefficient 값은 2πα(α;angle of attack), drag coefficient 값은 d\'Alembert\'s paradox 에 의하여 ‘0’ 이 된다.
Thin airfoil theorem 의 전개 가정 상 \'inviscid flow\'의 가정은 실험값과 이론값의 비교가 의미상 불가능함을 밝혀둔다.
Lift coefficient를 비교하면 이론값은 0도에서 실험값과 이론값이 0으로 같게 보정하였다. 그 상태에서 7도와 -7도의 lift coefficient의 이론값은 절대 값은 같으나, 부호가 다른 값으로서 0.767636과 -0.767636이며 Cp distribution을 통한 실험값에선 각각 0.690077과 -0.60209이다. 오차율은 각각 10~21%정도로 비교적 적은 값이 나왔다.
프로그램이론값
Cp 분포를 통한 실험값
오차율(%)
후류속도를 통한 실험값
AOA(deg)
Cl
Cd
Cl
Cd
/Cd
Cd
0
0
0.0103
0
0.035896
/
/0.162853
0.162853
7
0.767636
0.017
0.690077
0.08459
10.1036
/0.167009
0.167009
-7
-0.76764
0.017
-0.60209
0.029416
21.56568
/0.15822
0.15822
3.3 참고문헌을 통한 값과의 비교와 타당성 검증
=> 교수님께서 강의 하신 PPT의 보고서 분류에 따라서 각자의 개인 보고서에 수록하도록 했습니다.
4. Reference
ㆍ Frank M.White, Fluide Mechanics(번역) 5th edition, p.30 , McGrawHill, 2006
ㆍ John D.Anderson. Jr, Fundamental of Aerodynamics 4th edition, p210~p.213 McGrawHill
ㆍ http://www.aerospaceweb.org/question/airfoils/q0041.shtml
ㆍ John D.Anderson. Jr, Fundamental of Aerodynamics 4th edition ,p.319, McGrawHill
ㆍ John D.Anderson. Jr, Fundamental of Aerodynamics 4th edition, p.326 McGrawHill
ㆍ 상용 Program Design foil
ㆍ 상용 Program JAVA foil
angle of attack의 값과 airfoil의 geometry에 따라
이 때 airfoil의 형상을 살펴볼 때 thickness가 chord의 최대 12%이기 때문에 tangent를 근사시킬 수 있다.
따라서 우선 Free stream의 foil에 대한 수직성분은
가 된다.
두 번째로 살펴볼 값은 vortex로 발생하는 속도성분의 분석이다. chord line의 각 지점에 분포한 vortex에 의해 camber line위의 임의의 위치 x에 발생하는 수직속도를 라 할 때, airfoil의 camber line을 chord line으로 근사시킬 수 있으며
의 관계를 비로소 만족하게 된다.
미소 chord line 위의 vortex에 의한 수직속력의 미소성분은 다음과 같으며 이를 전 chord line에 대하여 적분을 한 값이 첫 번째로 구한 free stream의 foil 에 대한 수직속도와 같아야 한다.
--
이 때 NACA0012에 대하여 수식을 전개할 때 이 airfoil 은 대칭적인 형상이므로 camber line이 chord line이 일치하며 이 만족된다.
이 때 chord line 위의 원점으로부터의 길이를 (r,θ) coordinate로 변환하여 전개하면 (이 때 r의 중심은 chord line의 절반인 지점이다.)
의 관계가 얻어져 이를 준식에 적용하면
이 된다.
이를 Fourier transform을 이용하여 구하면 다음과 같다.
이는 아래의 증명에 의해 Kutta condition까지 만족시키는 것임을 알 수 있다.
이를 이용하여 chord line 전체의 circulation을 구하면
과 같고 Kutta-Koukowski theorem에 따라
이므로 이때의 lift coefficient를 구하면
이 된다.
-그림 참조- John D.Anderson. Jr, Fundamental of Aerodynamics 4th edition, p.326 McGrawHill
* 얇은 익형 이론을 이용한 항력
d\'Alembert\'s paradox
유체가 inviscid flow라고 가정했을 때,
∞를 free stream에 대한 첨자, s를 surface의 첨자라 하고
Bernoulli\'s equatinon에 의하면,
or ―(1)
여기서, 이고, 가 cylinder의 depth라고 하자.
(1)에서 유도된 를 위 식에 대입하여 적분을 하면, 에 대한 term에 의하여
(cylinder with circulation) = 0
이것이 d\'Alembert\'s paradox이다.
inviscid theory에 따르면, 유체의 free stream(uniform stream)에 잠겨 있는 어떠한 모양의 물체의 drag는 항상 0이다.
실제실험이 inviscid 상태가 아니기 때문에 inviscid 상태를 가정한 ‘얇은 익형 이론’ 을 적용할 수 없다. 따라서 우리는 상용프로그램에서 Cd 값을 구하여 분석해 보았다.
* 얇은 익형 이론을 이용한 값과 실험값과의 비교(두 가지 방법을 통한 값 모두 비교)
이론값
Cp 분포를 통한 실험값
Cl오차율(%)
후류속도를 통한 실험값
AOA(deg)
Cl
Cd
Cl
Cd
/
Cd
0
0
0
0
0.035896
/
/
0.162853
7
0.767636
0
0.690077
0.08459
10.1036
/
0.167009
-7
-0.76764
0
-0.60209
0.029416
21.56568
/
0.15822
위에서 정리하였듯이 이론값에 의하여 thin airfoil theory에서 lift coefficient 값은 2πα(α;angle of attack), drag coefficient 값은 d\'Alembert\'s paradox 에 의하여 ‘0’ 이 된다.
Thin airfoil theorem 의 전개 가정 상 \'inviscid flow\'의 가정은 실험값과 이론값의 비교가 의미상 불가능함을 밝혀둔다.
Lift coefficient를 비교하면 이론값은 0도에서 실험값과 이론값이 0으로 같게 보정하였다. 그 상태에서 7도와 -7도의 lift coefficient의 이론값은 절대 값은 같으나, 부호가 다른 값으로서 0.767636과 -0.767636이며 Cp distribution을 통한 실험값에선 각각 0.690077과 -0.60209이다. 오차율은 각각 10~21%정도로 비교적 적은 값이 나왔다.
프로그램이론값
Cp 분포를 통한 실험값
오차율(%)
후류속도를 통한 실험값
AOA(deg)
Cl
Cd
Cl
Cd
/Cd
Cd
0
0
0.0103
0
0.035896
/
/0.162853
0.162853
7
0.767636
0.017
0.690077
0.08459
10.1036
/0.167009
0.167009
-7
-0.76764
0.017
-0.60209
0.029416
21.56568
/0.15822
0.15822
3.3 참고문헌을 통한 값과의 비교와 타당성 검증
=> 교수님께서 강의 하신 PPT의 보고서 분류에 따라서 각자의 개인 보고서에 수록하도록 했습니다.
4. Reference
ㆍ Frank M.White, Fluide Mechanics(번역) 5th edition, p.30 , McGrawHill, 2006
ㆍ John D.Anderson. Jr, Fundamental of Aerodynamics 4th edition, p210~p.213 McGrawHill
ㆍ http://www.aerospaceweb.org/question/airfoils/q0041.shtml
ㆍ John D.Anderson. Jr, Fundamental of Aerodynamics 4th edition ,p.319, McGrawHill
ㆍ John D.Anderson. Jr, Fundamental of Aerodynamics 4th edition, p.326 McGrawHill
ㆍ 상용 Program Design foil
ㆍ 상용 Program JAVA foil
추천자료
 여성장애인의 성폭력
여성장애인의 성폭력 국제결혼
국제결혼 [인터넷중독]인터넷중독의 개념, 원인, 특징과 예방, 대응 및 회복 전략 분석(다양한 사례 중...
[인터넷중독]인터넷중독의 개념, 원인, 특징과 예방, 대응 및 회복 전략 분석(다양한 사례 중... 아동 청소년 가출
아동 청소년 가출  중퇴청소년 사례연구와 문제점 해결방안jo
중퇴청소년 사례연구와 문제점 해결방안jo 청소년 문화 요약, 정리
청소년 문화 요약, 정리 여성노동문제의 배경, 여성노동문제의 실태, 여성노동문제와 노동조건불일치문제, 여성노동문...
여성노동문제의 배경, 여성노동문제의 실태, 여성노동문제와 노동조건불일치문제, 여성노동문... 법제 - 기타법
법제 - 기타법 해외 선진국의 가정폭력, 성폭력 정책사례가 우리나라에게 주는 시사점
해외 선진국의 가정폭력, 성폭력 정책사례가 우리나라에게 주는 시사점 여성폭력의 개념, 원인, 법제도 및 정책현황
여성폭력의 개념, 원인, 법제도 및 정책현황 미혼모 발생요인 및 대책
미혼모 발생요인 및 대책 고용보험법 (고용보험법 정의, 고용보험법 목적, 고용보험제도, 고용보험 사업체계)
고용보험법 (고용보험법 정의, 고용보험법 목적, 고용보험제도, 고용보험 사업체계) [요약] 한국의 여성정책
[요약] 한국의 여성정책 청소년상담사의 정의와 필요성, 청소년상담사의 자격과 활동분야
청소년상담사의 정의와 필요성, 청소년상담사의 자격과 활동분야





















































소개글