본문내용
가해준 NaOH 양
pH
0
1.73
0.48
7.27
0.02
1.75
0.5
7.46
0.04
1.80
0.52
7.69
0.06
1.85
0.54
8.08
0.08
1.92
0.56
9.72
0.1
2.01
0.58
10.50
0.12
2.08
0.6
10.79
0.14
2.17
0.62
10.99
0.16
2.23
0.64
11.13
0.18
2.37
0.66
11.25
0.2
2.50
0.68
11.34
0.22
2.68
0.7
11.42
0.24
3.08
0.72
11.53
0.26
3.28
0.74
11.61
0.28
5.10
0.76
11.68
0.3
5.81
0.78
11.75
0.32
6.09
0.8
11.88
0.34
6.30
0.82
11.94
0.36
6.45
0.84
12.05
0.38
6.61
0.86
12.19
0.4
6.72
0.88
12.27
0.42
6.85
0.9
12.38
0.44
6.92
0.92
12.45
0.46
7.11
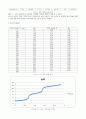
인산은 삼양성자 산이므로 세 개의 완충구간과 2개의 급격하게 바뀌는 당량점이 있다. 실험 결과를 통한 그래프도 그 사실을 보여주고 있다.
Discussion
1. 당량점과 완충구간을 표시해보자
2. 첫 번째 반 당량점, 두 번째 반 당량점, 세 번째 반당량점을 이용해 pKa1 pKa2 pKa3를 구해보자
NaOH 1몰에 1몰의 OH-를 내놓기 때문에 5N농도는 5M이다
0.1M 인산 20ml의 첫 번째 반 당량점에 이르려면 5N NaOH 몇 mL를 넣어야할까 ?
일단 첫 번째 당량점을 구하면
0.1M * 0.02 = 5 * X
X= 0.4mL
따라서 첫 번째 반 당량점은 0.2mL이다 .
NaOH 0.2mL를 넣었을때 pH를 위 표에서 구하면 2.5이다. 인산의 pKa1이 첫 번째 반당량점의 pH와 같다.
따라서 -log(Ka1)=2.5
따라서 Ka1은 3.16*10^-3으로 계산된다.
실제 인산의 Ka1 값은 7.25×103로 이론적 pH는 2.14이다. 따라서 실험과 비슷하다고 볼 수 있다.
따라서 두 번째 반 당량점은 0.6mL가 되어야하는데 그래프상에서도 조금 차이가 있다
따라서 그래프를 통해 반당량점을 두 번째 찾으면 약 0.46정도 된다. 이때 pH는 7.11이다
위와 같이 공식을 세우면 -log(Ka2)=7.11
--> Ka2 = 7.76*10^-8으로 나온다
이론적 Ka2 값은 6.31*10^-8이고 이를 통한 pH는 약 7.19정도 되므로 실험값과 비슷하다
세 번째 반당량점은 계산을 해보면 1mL로 예상되는데 그에 해당하는 실험까지 하지 않았다.
따라서 가장 마지막은 0.92mL로 해보면 약 Ka3 = 3.548*10^-13이고 이론값은 3.98*10^-13으로 1mL까지 측정한다면 거의 유사하게 나올것이다.
3. 헨더슨 하셀바하 식을 유도 해보자.
4. 반 당량점에서 pH=pKa 인 이유는?
반당량점에서는 [A-] = [HA] ㅣ이다. log1=0이므로 pH=pKa가 된다.
5. 강산 강염기로는 완충용액을 만들 수 없는 이유는 무엇인가?
완충용액의 역할은 급격한 pH변화에 대응하는 것이다. 그래서 사용하는 물질들의 이온화도가 낮아야 한다. 그래야 주변에서 들어오는 H+나 OH-에 반응해서 조금씩 이온화를 하며 평형을 유지하는데 결과적으로 용액 전체의 pH가 큰 변화없이 유지한다.
강산 강염기는 이 이온화도가 매우 크다. 그러기 때문에 물에 들어가면 싹 다 이온화하기 때문에 넣는 족족 바로 해리되므로 평형을 논할 수 없으며 완충 용액을 만들 수 없다.
Reference
-옥스토비의 일반화학 6판 , David W. OXTOBY
-위키피디아
-연세대학교 시스템생물학과
pH
0
1.73
0.48
7.27
0.02
1.75
0.5
7.46
0.04
1.80
0.52
7.69
0.06
1.85
0.54
8.08
0.08
1.92
0.56
9.72
0.1
2.01
0.58
10.50
0.12
2.08
0.6
10.79
0.14
2.17
0.62
10.99
0.16
2.23
0.64
11.13
0.18
2.37
0.66
11.25
0.2
2.50
0.68
11.34
0.22
2.68
0.7
11.42
0.24
3.08
0.72
11.53
0.26
3.28
0.74
11.61
0.28
5.10
0.76
11.68
0.3
5.81
0.78
11.75
0.32
6.09
0.8
11.88
0.34
6.30
0.82
11.94
0.36
6.45
0.84
12.05
0.38
6.61
0.86
12.19
0.4
6.72
0.88
12.27
0.42
6.85
0.9
12.38
0.44
6.92
0.92
12.45
0.46
7.11
인산은 삼양성자 산이므로 세 개의 완충구간과 2개의 급격하게 바뀌는 당량점이 있다. 실험 결과를 통한 그래프도 그 사실을 보여주고 있다.
Discussion
1. 당량점과 완충구간을 표시해보자
2. 첫 번째 반 당량점, 두 번째 반 당량점, 세 번째 반당량점을 이용해 pKa1 pKa2 pKa3를 구해보자
NaOH 1몰에 1몰의 OH-를 내놓기 때문에 5N농도는 5M이다
0.1M 인산 20ml의 첫 번째 반 당량점에 이르려면 5N NaOH 몇 mL를 넣어야할까 ?
일단 첫 번째 당량점을 구하면
0.1M * 0.02 = 5 * X
X= 0.4mL
따라서 첫 번째 반 당량점은 0.2mL이다 .
NaOH 0.2mL를 넣었을때 pH를 위 표에서 구하면 2.5이다. 인산의 pKa1이 첫 번째 반당량점의 pH와 같다.
따라서 -log(Ka1)=2.5
따라서 Ka1은 3.16*10^-3으로 계산된다.
실제 인산의 Ka1 값은 7.25×103로 이론적 pH는 2.14이다. 따라서 실험과 비슷하다고 볼 수 있다.
따라서 두 번째 반 당량점은 0.6mL가 되어야하는데 그래프상에서도 조금 차이가 있다
따라서 그래프를 통해 반당량점을 두 번째 찾으면 약 0.46정도 된다. 이때 pH는 7.11이다
위와 같이 공식을 세우면 -log(Ka2)=7.11
--> Ka2 = 7.76*10^-8으로 나온다
이론적 Ka2 값은 6.31*10^-8이고 이를 통한 pH는 약 7.19정도 되므로 실험값과 비슷하다
세 번째 반당량점은 계산을 해보면 1mL로 예상되는데 그에 해당하는 실험까지 하지 않았다.
따라서 가장 마지막은 0.92mL로 해보면 약 Ka3 = 3.548*10^-13이고 이론값은 3.98*10^-13으로 1mL까지 측정한다면 거의 유사하게 나올것이다.
3. 헨더슨 하셀바하 식을 유도 해보자.
4. 반 당량점에서 pH=pKa 인 이유는?
반당량점에서는 [A-] = [HA] ㅣ이다. log1=0이므로 pH=pKa가 된다.
5. 강산 강염기로는 완충용액을 만들 수 없는 이유는 무엇인가?
완충용액의 역할은 급격한 pH변화에 대응하는 것이다. 그래서 사용하는 물질들의 이온화도가 낮아야 한다. 그래야 주변에서 들어오는 H+나 OH-에 반응해서 조금씩 이온화를 하며 평형을 유지하는데 결과적으로 용액 전체의 pH가 큰 변화없이 유지한다.
강산 강염기는 이 이온화도가 매우 크다. 그러기 때문에 물에 들어가면 싹 다 이온화하기 때문에 넣는 족족 바로 해리되므로 평형을 논할 수 없으며 완충 용액을 만들 수 없다.
Reference
-옥스토비의 일반화학 6판 , David W. OXTOBY
-위키피디아
-연세대학교 시스템생물학과
키워드
추천자료
 0.1N-질산은(AgNO3) 표준용액의 조제 및 염화물의 정량
0.1N-질산은(AgNO3) 표준용액의 조제 및 염화물의 정량 [자연과학] pH Titeration(PH 적정)과 완충용액
[자연과학] pH Titeration(PH 적정)과 완충용액 0.1N-NaCl 및 0.1N-AgNO3 표준용액
0.1N-NaCl 및 0.1N-AgNO3 표준용액 Preparation and standardization of 0.1N-HCl 0.1 N 염산 표준용액의 조제 및 표준화
Preparation and standardization of 0.1N-HCl 0.1 N 염산 표준용액의 조제 및 표준화 [실험보고서] 인산의 적정과 완충용액
[실험보고서] 인산의 적정과 완충용액 [일반화학실험][예비+결과] 인산의 적정과 완충용액 실험
[일반화학실험][예비+결과] 인산의 적정과 완충용액 실험 [분석화학] 산염기의 표준용액 제조와 표정[Preparing Standard Acid and Base]
[분석화학] 산염기의 표준용액 제조와 표정[Preparing Standard Acid and Base] 화학 - pH 와 완충 용액에 대해
화학 - pH 와 완충 용액에 대해 [식품분석실험] 표준용액의 제조와 규정도계수를 이용한 표정
[식품분석실험] 표준용액의 제조와 규정도계수를 이용한 표정 일반화학실험 -인산의 적정과 완충 용액
일반화학실험 -인산의 적정과 완충 용액 일반화학실험 - 산 및 알칼리 표준용액의 조제 및 적정
일반화학실험 - 산 및 알칼리 표준용액의 조제 및 적정 [실험보고서] HBCD 용액 CRM 단기안정도 실험
[실험보고서] HBCD 용액 CRM 단기안정도 실험 [생물학실험 보고서] 용액제조 및 실험기기 사용법
[생물학실험 보고서] 용액제조 및 실험기기 사용법 실험기구 사용법 및 용액 제조하기(예비 레포트)
실험기구 사용법 및 용액 제조하기(예비 레포트)




























소개글